Multivariate chain rule
Before reading this guide, it is recommended that you read Guide: Introduction to partial differentiation and Guide: The chain rule.
| Narration of study guide: |
What is the multivariate chain rule?
As seen in Guide: The chain rule, the chain rule tells you how to differentiate a function \(y=y(x)\) with respect to another variable \(t\) when \(x\) depends on \(t\). \[\dfrac{\mathrm{d}y}{\mathrm{d}t} = \dfrac{\mathrm{d}y}{\mathrm{d}x}\dfrac{\mathrm{d}x}{\mathrm{d}t}\]
This rule can be extended to functions of multiple variables through the multivariate chain rule. The extended rule tells you how to compute derivatives of composite functions (functions of functions) involving multiple variables. It allows you to track how changes in independent variables influence a final quantity through intermediate variables called dependent variables.
The multivariate chain rule is used in problems involving parametric multivariate functions, such as those describing motion along curved surfaces, transformations in computer graphics, and population models where growth depends on multiple time-varying factors. Another important example is a climate model: these use variables like temperature, humidity and ocean currents to predict weather patterns.
Before beginning, it is important to understand the difference between dependent and independent variables. From there, the multivariate chain rule accounts for any combination of dependent and independent variables; this guide looks at two dependent variables with one/two independent variables, and then discusses the general case at the very end.
Dependent and independent variables
When a function depends on a specific variable, this means that the function is written with the variable in its rule. For example, the function \(f(x,y) = x^2 + y^2\) depends on \(x\) and \(y\) as the function is written in terms of \(x\) and \(y\).
A multivariate (or multivariable) function is a function that depends on more than one variable.
Consider a multivariate function \(w = w(x,y,z) = 2x^2 + xy + 3xz\) where \[\begin{aligned} x(s,t) &= s^2 - t \\[0.2em] y(s,t) &= s^2 + t \\[0.2em] z(s,t) &= 2s + t^2 \end{aligned}\]
The variables \(x\), \(y\) and \(z\) are referred to as dependent variables as they are functions that depend on (can be written in terms of) the variables \(s\) and \(t\). Even though \(x\), \(y\) and \(z\) are referred to as ‘variables’, they are actually functions of the variables \(s\) and \(t\). In this case, the dependent variables can be written in functional form as \(x = x(s,t)\), \(y = y(s,t)\) and \(z = z(s,t)\) to emphasize dependency.
The variables \(s\) and \(t\) are referred to as independent variables as they do not depend on any other variables.
Occasionally, the dependent variables in this guide may be referred to as intermediate variables since they connect the independent variables \(s\) and \(t\) to the final quantity \(w\).
Functions of two dependent variables with one independent variable
Suppose you have a function \(z = z(x,y)\). Here, \(z\) depends on two dependent variables \(x\) and \(y\), however both \(x\) and \(y\) are functions of a single independent variable \(t\). \[x=x(t) \quad \textsf{and} \quad y=y(t)\]
This means that, even though \(z\) initially looks like a function of two dependent variables \(x\) and \(y\), it really depends on a single independent variable \(t\). You can write \(z\) entirely in terms of \(t\): \[z = z(x(t),y(t))\]
The goal is to find \(\dfrac{\mathrm{d}z}{\mathrm{d}t}\).
You may not be able to differentiate \(z = z(x,y)\) directly with respect to \(t\) because \(z\) depends intermediately on both \(x\) and \(y\). Instead, you could use the multivariate chain rule.
Let \(z=z(x,y)\) where \(f\) is a differentiable function of \(x\) and \(y\). Also let \(x=x(t)\) and \(y=y(t)\) be differentiable functions of \(t\).
The function \(z\) can then be differentiated with respect to \(t\) according to \[\dfrac{\mathrm{d}z}{\mathrm{d}t} = \dfrac{\partial z}{\partial x}\dfrac{\mathrm{d}x}{\mathrm{d}t} + \dfrac{\partial z}{\partial y}\dfrac{\mathrm{d}y}{\mathrm{d}t}\]
The left-most derivative \(\dfrac{\mathrm{d}z}{\mathrm{d}t}\) is written with a straight \(\mathrm{d}\) as \(z= z(x,y) = z(x(t),y(t))\) is ultimately a function of \(t\) alone. Here, \(z\) is written using the expressions for \(x\) and \(y\) in terms of \(t\).
Derivatives such as \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{\partial y}\) are written with a curly \(\partial\) as \(z\) is a function that depends on two variables \(x\) and \(y\).
Derivatives such as \(\dfrac{\mathrm{d}x}{\mathrm{d}t}\) and \(\dfrac{\mathrm{d}y}{\mathrm{d}t}\) are written with a straight \(\mathrm{d}\) as \(x\) is a function that depends only on a single variable \(t\).
As \(t\) changes, both dependent variables \(x\) and \(y\) change as they are both functions of the independent variable \(t\). This causes \(z\) to change as it is a function of the variables \(x\) and \(y\) which are also changing.
Let \(z = z(x,y) = x^3 + y^3\) where \(x=3t^2\) and \(y=\cos(t)\). Use the multivariate chain rule to find \(\dfrac{\mathrm{d}z}{\mathrm{d}t}\).
First, calculate the derivatives required for the multivariate chain rule. \[\begin{array}{lcl} \dfrac{\partial z}{\partial x} = 3x^2 & \quad & \dfrac{\partial z}{\partial y} = 3y^2 \\[0.5em] \dfrac{\mathrm{d}x}{\mathrm{d}t} = 6t & \quad & \dfrac{\mathrm{d}y}{\mathrm{d}t} = -\sin(t) \end{array}\]
You then need to substitute the derivatives into the multivariate chain rule, then substitute for \(x=3t^2\) and \(y=\cos(t)\). \[\begin{aligned} \dfrac{\mathrm{d}z}{\mathrm{d}t} &= \dfrac{\partial z}{\partial x}\dfrac{\mathrm{d}x}{\mathrm{d}t} + \dfrac{\partial z}{\partial y}\dfrac{\mathrm{d}y}{\mathrm{d}t} \\[0.5em] &= (3x^2)(6t) + (3y^2)(-\sin(t)) \\[0.5em] &= 3(3t^2)^2(6t) + 3(\cos(t))^2(-\sin(t)) \\[0.5em] &= 162t^5 - 3\sin(t)\cos^2(t) \end{aligned}\] and this is your final answer.
Make sure that your final answer is always expressed only in terms of the independent variables. Your final answer should not include any intermediate variables (like \(x\) and \(y\) in this example).
You could notice that in this case, you could substitute \(x = x(t)\) and \(y = y(t)\) into the equation and directly differentiate with respect to \(t\). However, this might not be possible in all cases, and usually using the multivariate chain rule will result in cleaner working. For instance, if \(z=z(x,y) = xe^{xy}\) with dependent variables \(x(t) = t^5 - t^4 + t^3 + 1\) and \(y(t) = \cos(t^2)\), then you can directly substitute and differentiate; but it would be very difficult to do!
Functions of two dependent variables with two independent variables
Suppose you have a function \(z=z(x,y)\), where both \(x\) and \(y\) are now functions of two independent variables. Here, \(z\) depends on two dependent variables \(x\) and \(y\), however now both \(x\) and \(y\) are functions of two independent variables \(s\) and \(t\). \[x=x(s,t) \quad \textsf{and} \quad y=y(s,t)\]
This means that, even though \(z\) initially looks like a function of two dependent variables \(x\) and \(y\), it really depends on two independent variables \(s\) and \(t\). In fact, you can write \(z\) entirely in terms of \(s\) and \(t\). \[z = z ( x(s,t), y(s,t) )\]
Since there are now two independent variables, the goal is to find both \(\dfrac{\partial z}{\partial s}\) and \(\dfrac{\partial z}{\partial t}\).
You cannot differentiate \(z = z(x,y)\) directly with respect to \(s\) or \(t\) because \(z\) depends intermediately on both \(x\) and \(y\). Instead, you need to use the multivariate chain rule.
Let \(z=z(x,y)\) where \(f\) is a differentiable function of \(x\) and \(y\). Also, let \(x=x(s,t)\) and \(y=y(s,t)\) be differentiable functions of \(s\) and \(t\).
The function \(z\) can then be differentiated with respect to \(s\) and \(t\) with \[\begin{aligned} \dfrac{\partial z}{\partial s} &= \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial s} + \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial s} \\[0.5em] \dfrac{\partial z}{\partial t} &= \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial t} + \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial t} \end{aligned}\]
The left-most derivatives \(\dfrac{\partial z}{\partial s}\) and \(\dfrac{\partial z}{\partial t}\) are written with a curly \(\partial\) as \(z=z(s,t)\) is considered a function of both \(s\) and \(t\) at this stage. Here, \(z\) is written using the expressions for \(x\) and \(y\) in terms of \(s\) and \(t\).
Notice that the \(\dfrac{\partial x}{\partial s}\), \(\dfrac{\partial x}{\partial t}\), \(\dfrac{\partial y}{\partial s}\) and \(\dfrac{\partial y}{\partial t}\) derivatives are now written with a curly \(\partial\) instead of a straight \(\mathrm{d}\) as \(x\) and \(y\) are functions that now depend on two independent variables \(s\) and \(t\). This means the derivatives are now partial derivatives instead of ordinary derivatives.
As \(s\) and \(t\) change, both dependent variables \(x\) and \(y\) change as they are both functions of the independent variables \(s\) and \(t\). This causes \(z\) to change as it is a function of variables \(x\) and \(y\) which are also changing.
Let \(z = z(x,y) = x^2 + 3xy\) where \(x=s+t^2\) and \(y=s^2-t\). Use the multivariate chain rule to find \(\dfrac{\partial z}{\partial s}\) and \(\dfrac{\partial z}{\partial t}\).
First, calculate the derivatives required for the multivariate chain rule. \[\begin{array}{lcl} \dfrac{\partial z}{\partial x} = 2x + 3y & \quad & \dfrac{\partial z}{\partial y} = 3x \\[0.5em] \dfrac{\partial x}{\partial s} = 1 & \quad & \dfrac{\partial y}{\partial s} = 2s \\[0.5em] \dfrac{\partial x}{\partial t} = 2t & \quad & \dfrac{\partial y}{\partial t} = -1 \end{array}\]
You need to substitute the partial derivatives into the multivariate chain rule, then substitute for \(x=s+t^2\) and \(y=s^2-t\).
Firstly, calculate the partial derivative of \(z\) with respect to \(s\): \[\begin{aligned} \dfrac{\partial z}{\partial s} &= \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial s} + \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial s} \\[0.5em] &= (2x+3y)(1) + (3x)(2s) \\[0.5em] &= ( 2(s+t^2)+3(s^2-t) ) ( 1 ) + ( 3(s+t^2) ) ( 2s ) \\[0.5em] &= 9s^2 + 2t^2 + 6st^2 + 2s - 3t \end{aligned}\]
Now, calculate the partial derivative of \(z\) with respect to \(t\): \[\begin{aligned} \dfrac{\partial z}{\partial t} &= \dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial t} + \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial t} \\[0.5em] &= (2x+3y)(2t) + (3x)(-1) \\[0.5em] &= ( 2(s+t^2)+3(s^2-t) ) ( 2t ) + ( 3(s+t^2) ) ( -1 ) \\[0.5em] &= 4t^3-9t^2+6s^2t-3s+4st \end{aligned}\]
Generalized multivariate chain rule
Suppose you have a function \(w = w(x_1, x_2, \ldots , x_n)\). Here, \(w\) depends on \(n\) dependent variables \(x_1, x_2, \ldots, x_n\) where each of these variables is a function of \(m\) independent variables \(t_1, t_2, \ldots, t_m\). \[\begin{aligned} x_1 &= x_1(t_1, t_2, \ldots, t_m) \\[0.2em] x_2 &= x_2(t_1, t_2, \ldots, t_m) \\[0.2em] \vdots \;\, &= \;\, \vdots \\[0.2em] x_n &= x_n(t_1, t_2, \ldots, t_m) \end{aligned}\]
The previous cases investigated were \[\begin{array}{lclclclclcl} \textsf{Case 1:} & \; & n = 1, & \; & m = 1, & \; & y = y(x), & \; & x = x(t). & \; & \\[0.5em] \textsf{Case 2:} & \; & n = 2, & \; & m = 1, & \; & z = z(x, y), & \; & x = x(t), & \; & y = y(t). \\[0.5em] \textsf{Case 3:} & \; & n = 2, & \; & m = 2, & \; & z = z(x, y), & \; & x = x(s, t), & \; & y = y(s, t). \end{array}\]
where:
Case 1 corresponds to the chain rule for one dependent variable and one independent variable - see Guide: The chain rule.
Case 2 corresponds to the chain rule for two dependent variables and one independent variable.
Case 3 corresponds to the chain rule for two dependent variables and two independent variables.
The multivariate chain rule can be generalized as follows.
Let \(w = w(x_1, x_2, \ldots , x_n)\) be a differentiable function of \(x_1, x_2, \ldots, x_n\). Also let the following dependent variables be differentiable functions of \(t_1, t_2, \ldots, t_m\). \[\begin{aligned} x_1 &= x_1(t_1, t_2, \ldots, t_m) \\[0.2em] x_2 &= x_2(t_1, t_2, \ldots, t_m) \\[0.2em] \vdots \;\, &= \;\, \vdots \\[0.2em] x_n &= x_n(t_1, t_2, \ldots, t_m) \end{aligned}\]
The function \(w\) can then be differentiated with respect to \(t_1, t_2, \ldots, t_m\) with \[\begin{aligned} \dfrac{\partial w}{\partial t_1} &= \sum_{i=1}^n \dfrac{\partial w}{\partial x_i} \dfrac{\partial{x_i}}{\partial {t_1}} = \dfrac{\partial w}{\partial x_1} \dfrac{\partial x_1}{\partial t_1} + \dfrac{\partial w}{\partial x_2} \dfrac{\partial x_2}{\partial t_1} + \ldots + \dfrac{\partial w}{\partial x_n} \dfrac{\partial x_n}{\partial t_1} \\[0.5em] \dfrac{\partial w}{\partial t_2} &= \sum_{i=1}^n \dfrac{\partial w}{\partial x_i} \dfrac{\partial{x_i}}{\partial {t_2}} = \dfrac{\partial w}{\partial x_1} \dfrac{\partial x_1}{\partial t_2} + \dfrac{\partial w}{\partial x_2} \dfrac{\partial x_2}{\partial t_2} + \ldots + \dfrac{\partial w}{\partial x_n} \dfrac{\partial x_n}{\partial t_2} \\[0.5em] \vdots \quad\! &= \quad\! \vdots \\[0.5em] \dfrac{\partial w}{\partial t_m} &= \sum_{i=1}^n \dfrac{\partial w}{\partial x_i} \dfrac{\partial{x_i}}{\partial {t_m}} = \dfrac{\partial w}{\partial x_1} \dfrac{\partial x_1}{\partial t_m} + \dfrac{\partial w}{\partial x_2} \dfrac{\partial x_2}{\partial t_m} + \ldots + \dfrac{\partial w}{\partial x_n} \dfrac{\partial x_n}{\partial t_m} \end{aligned}\]
(where \(\sum\) represents sigma notation; see Guide: Sigma notation for more.)
A particular case exists where the variables \(x_i\) each depend on only one independent variable \(x_1 = x_1(t), x_2 = x_2(t), \ldots, x_n = x_n(t)\). In this case, a straight \(\mathrm{d}\) should be used instead of a curly \(\partial\). \[ \begin{aligned} \dfrac{\mathrm{d}{w}}{\mathrm{d}{t}} &=\sum_{i=1}^n \dfrac{\partial w}{\partial x_i} \dfrac{\mathrm{d}{x_i}}{\mathrm{d}{t}} = \dfrac{\partial w}{\partial x_1} \dfrac{\mathrm{d}{x_1}}{\mathrm{d}{t}} + \dfrac{\partial w}{\partial x_2} \dfrac{\mathrm{d}{x_2}}{\mathrm{d}{t}} + \ldots + \dfrac{\partial w}{\partial x_n} \dfrac{\mathrm{d}{x_n}}{\mathrm{d}{t}}\\[0.5em] \end{aligned} \]
Similarly, if there is only one dependent variable \(x\), then a straight \(\mathrm{d}\) should be used instead of a curly \(\partial\) for the derivatives of \(w\) with respect to \(x\).
Here’s an example of a case with \(n=3\) dependent variables and \(m=2\) independent variables.
Let \(w = w(x,y,z) = x^2 -3xz + 2xy\) where \[\begin{aligned} x(s,t) &= s^2-t \\ y(s,t) &= s\cos(t) \\ z(s,t) &= t^2-s \end{aligned}\]
Use the multivariate chain rule to find \(\dfrac{\partial w}{\partial s}\) and \(\dfrac{\partial w}{\partial t}\).
Firstly, calculate the derivatives required for the multivariate chain rule. \[\begin{array}{lclcl} \dfrac{\partial w}{\partial x} = 2x - 3z + 2y & \quad & \dfrac{\partial w}{\partial y} = 2x & \quad & \dfrac{\partial w}{\partial z} = -3x \\[0.5em] \dfrac{\partial x}{\partial s} = 2s & \quad & \dfrac{\partial y}{\partial s} = \cos(t) & \quad & \dfrac{\partial z}{\partial s} = -1 \\[0.5em] \dfrac{\partial x}{\partial t} = -1 & \quad & \dfrac{\partial y}{\partial t} = -s\sin(t) & \quad & \dfrac{\partial z}{\partial t} = 2t \end{array}\]
You need to substitute the partial derivatives into the multivariate chain rule, then substitute for \(x=s^2-t\), \(y = s\cos(t)\) and \(z=t^2-s\).
You can calculate the partial derivative of \(w\) with respect to \(s\) as: \[\begin{aligned} \dfrac{\partial w}{\partial s} &= \dfrac{\partial w}{\partial x}\dfrac{\partial x}{\partial s} + \dfrac{\partial w}{\partial y}\dfrac{\partial y}{\partial s} + \dfrac{\partial w}{\partial z}\dfrac{\partial z}{\partial s} \\[0.5em] &= (2x-3z+2y)(2s) + (2x)(\cos(t)) + (-3x)(-1) \\[1em] &= ( 2(s^2-t)-3(t^2-s)+2s\cos(t) ) ( 2s ) + ( 2(s^2-t) ) ( \cos(t) ) \\ &\phantom{= } \quad + ( -3(s^2-t) ) ( -1 ) \\[1em] &= 4s^3 + 9s^2 + 6s^2\cos(t) - 4st - 6st^2 - 2t\cos(t) - 3t \end{aligned}\]
You can calculate the partial derivative of \(w\) with respect to \(t\) as: \[\begin{aligned} \dfrac{\partial w}{\partial t} &= \dfrac{\partial w}{\partial x}\dfrac{\partial x}{\partial t} + \dfrac{\partial w}{\partial y}\dfrac{\partial y}{\partial t} + \dfrac{\partial w}{\partial z}\dfrac{\partial z}{\partial t} \\[0.5em] &= (2x-3z+2y)(-1) + (2x)(-s\sin(t)) + (-3x)(2t) \\[1em] &= ( 2(s^2-t)-3(t^2-s)+2s\cos(t) ) ( -1 ) \\ &\phantom{= } \quad + ( 2(s^2-t) ) ( -s\sin(t) ) + ( -3(s^2-t) ) ( 2t ) \\[1em] &= -2s^2 + 9t^2 + 2t - 3s - 2s\cos(t) - 2s^3\sin(t) \\ &\phantom{= } \quad + 2st\sin(t) - 6ts^2 \end{aligned}\]
Tree representation of the multivariate chain rule
There is a useful way for determining the required form of the multivariate chain rule without needing to remember the generalized rule above. The following diagram is a tree representation of the dependencies between variables in a multivariate function.
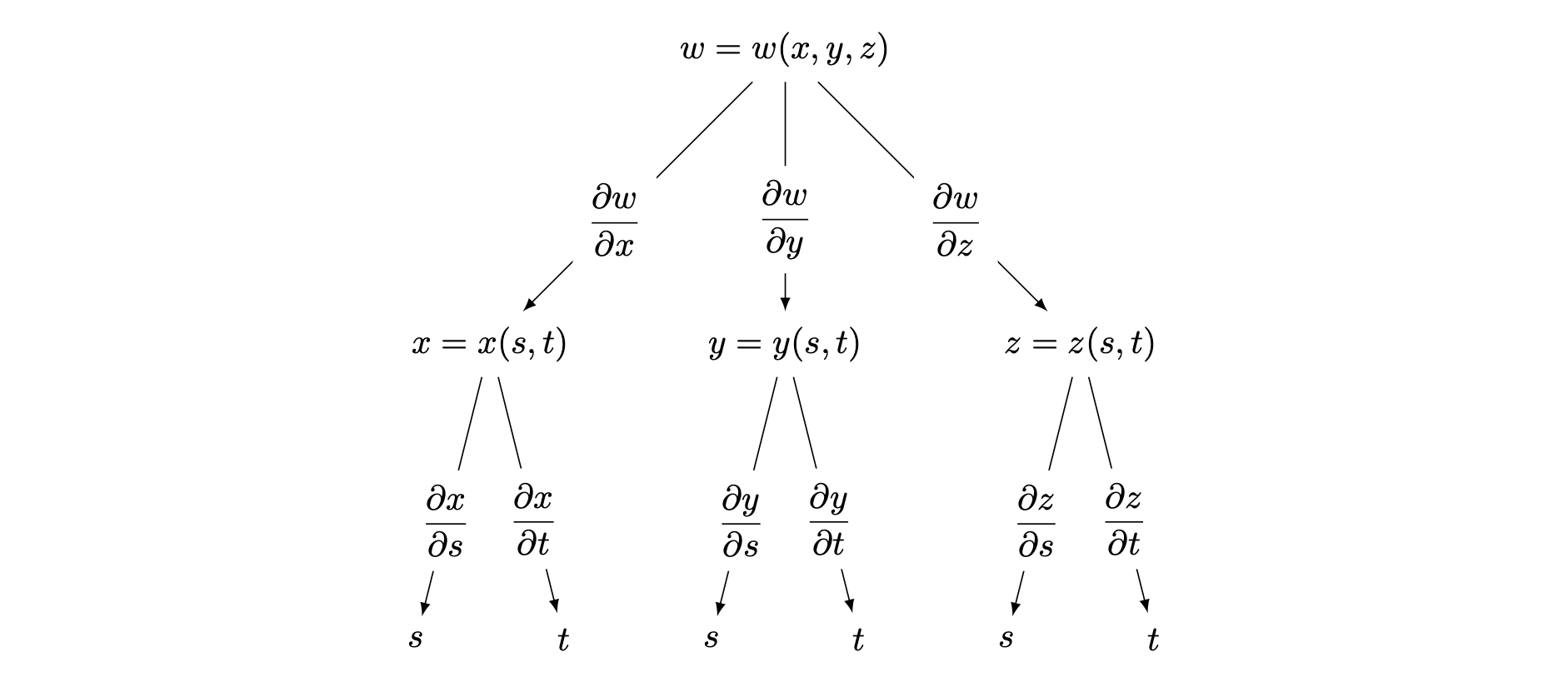
At the top of the tree is the function \(w = w(x,y,z)\), which depends on three intermediate variables \(x\), \(y\) and \(z\). Each of these three intermediate variables depend on independent variables \(s\) and \(t\). The tree shows all possible paths from \(w\) to the independent variables \(s\) and \(t\).
Each path represents a chain of partial differentiation (a product of partial derivatives) when applying the chain rule. All paths are combined by summing these chains at the end to find the complete partial derivative of \(w\) with respect to the relevant independent variable.
To find \(\dfrac{\partial w}{\partial s}\), follow all paths leading from \(z\) to \(s\). \[\begin{array}{rcl} \textsf{Path via } x \textsf{:} & & \dfrac{\partial w}{\partial x} \dfrac{\partial x}{\partial s} \\[0.5em] \textsf{Path via } y \textsf{:} & & \dfrac{\partial w}{\partial y} \dfrac{\partial y}{\partial s} \\[0.5em] \textsf{Path via } z \textsf{:} & & \dfrac{\partial w}{\partial z} \dfrac{\partial z}{\partial s} \\[0.5em] \textsf{Combine all terms:} & & \dfrac{\partial w}{\partial x} \dfrac{\partial x}{\partial s} + \dfrac{\partial w}{\partial y} \dfrac{\partial y}{\partial s} + \dfrac{\partial w}{\partial z} \dfrac{\partial z}{\partial s} = \dfrac{\partial w}{\partial s} \end{array}\]
You can perform a similar method to find \(\dfrac{\partial w}{\partial t}\).
Remember that if a variable has only a single dependency on another variable (no separate branch), a straight \(\mathrm{d}\) should be used in the derivative instead of a curly \(\partial\).
Quick check problems
- Which of the following correctly describes a dependent variable?
- Consider the function \(z = z(x,y) = x^2 + y^2\) where \(x = 2t\) and \(y = 3t\).
There is/are dependent variable(s) and independent variable(s).
The required form of the multivariate chain rule is \[\dfrac{\mathrm{d}z}{\mathrm{d}t} = \dfrac{\partial z}{\partial x} \dfrac{\mathrm{d}x}{\mathrm{d}t} + \dfrac{\partial z}{\partial y} \dfrac{\mathrm{d}y}{\mathrm{d}t}\]
The partial derivative of \(z\) with respect to \(x\) is \(\dfrac{\partial z}{\partial x} =\) .
The full derivative of \(x\) with respect to \(t\) is \(\dfrac{\mathrm{d}x}{\mathrm{d}t} =\) .
The partial derivative of \(z\) with respect to \(y\) is \(\dfrac{\partial z}{\partial y} =\) .
The full derivative of \(y\) with respect to \(t\) is \(\dfrac{\mathrm{d}y}{\mathrm{d}t} =\) .
Use the multivariate chain rule to find the full derivative of \(z\) with respect to \(t\), expressing your answer in terms of \(t\) only. \(\dfrac{\mathrm{d}z}{\mathrm{d}t} =\)
Further reading
For more questions on the subject, please go to Questions: Multivariate chain rule.
For a way to differentiate implicit functions of more than one variable, please see Guide: Multivariate implicit differentiation.
Version history
v1.0: initial version created 05/25 by Donald Campbell as part of a University of St Andrews VIP project.