Introduction to radians
| Narration of study guide: |
What are radians?
Radians, like degrees are a way of measuring the size of angles and can often be identified by the presence of \(\pi\).
Radians are the SI unit for angles derived from the radius of a circle, which makes them especially useful when working with circles. You will see this relationship more in the following section on arc length and sector area. Radians are denoted by the symbol rad, or sometimes by \(^c\) (although this is slightly older).
Radians are exclusively used to describe angles in calculus; therefore if you want to study calculus in the future it is extremely important to understand how to convert between degrees and radians, and be comfortable using radians more generally.
This guide will firstly describe the relationship between radians and circles. Then it will describe the relationship between radians and degrees showing how to convert between them. Lastly, it will provide a table of some useful degree to radians conversions for common angle sizes.
Radians and circles
Before you see the close relationship between radians and circles, it s important to understand what arcs and sectors are.
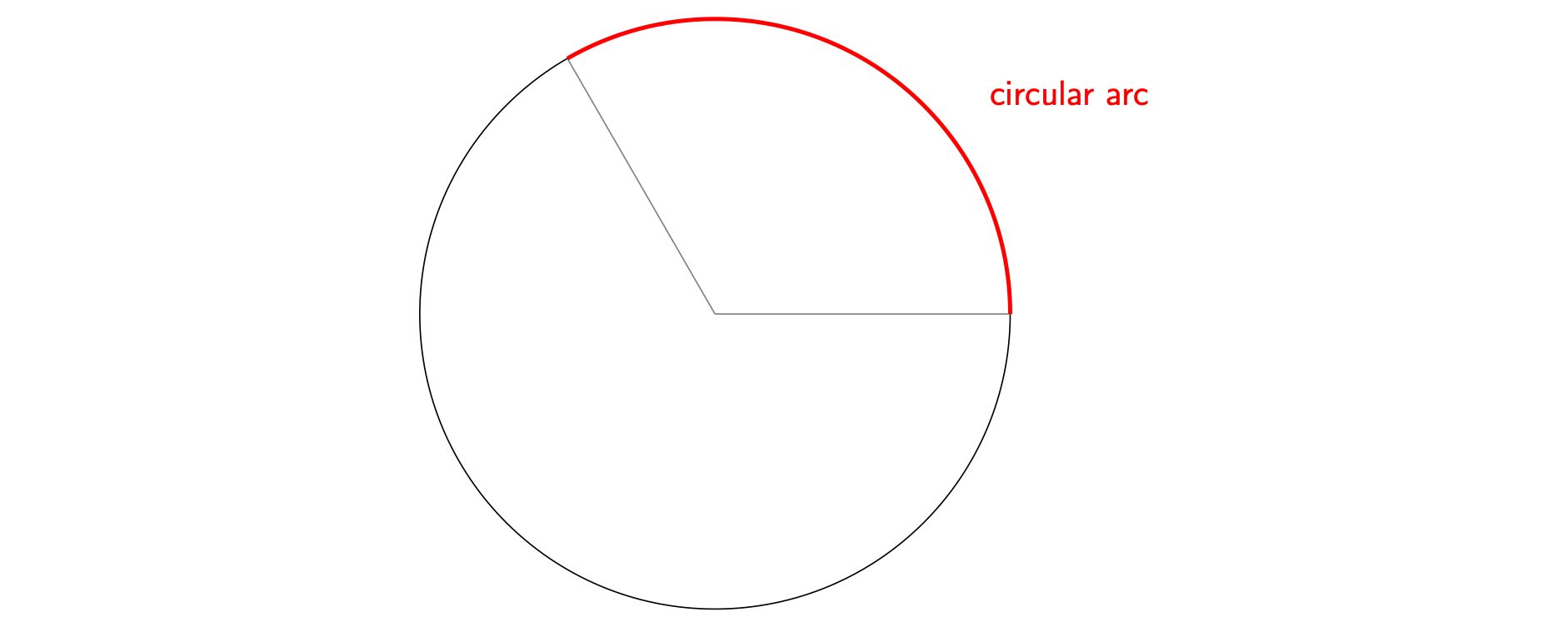
Pick any two different points on a circle and draw a curve between them, following the circle. This curve is known as a circular arc, but this is usually shortened to arc.
A circle does not include the interior of the circle. A circle together with its interior is called a disk.
Figure 1 shows an example of an arc.
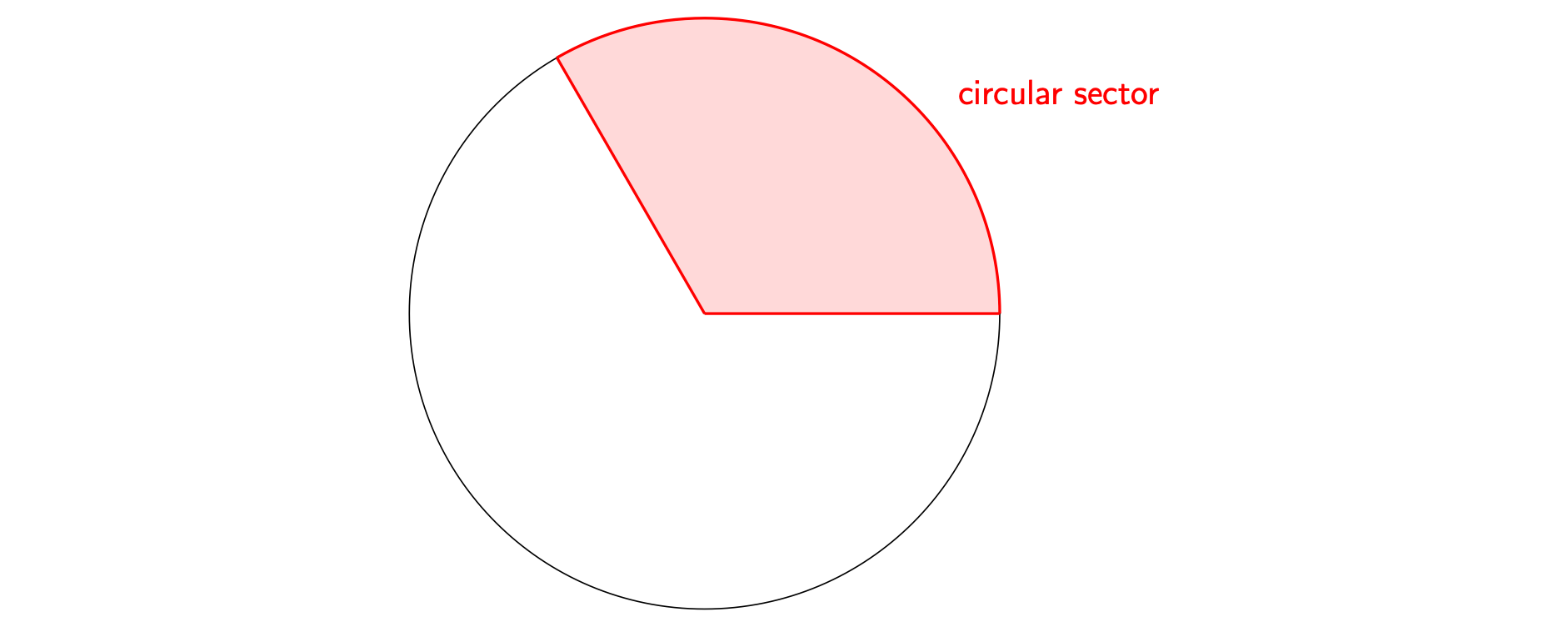
Pick two different points on a circle and draw two radiuses between them and the centre. The area enclosed by these two radiuses of the circle and the arc between the points is called a circular sector, but this is usually shortened to sector.
Figure 2 is an example of a sector.
These two concepts form the foundations to to precisely explain the definition of a radian.
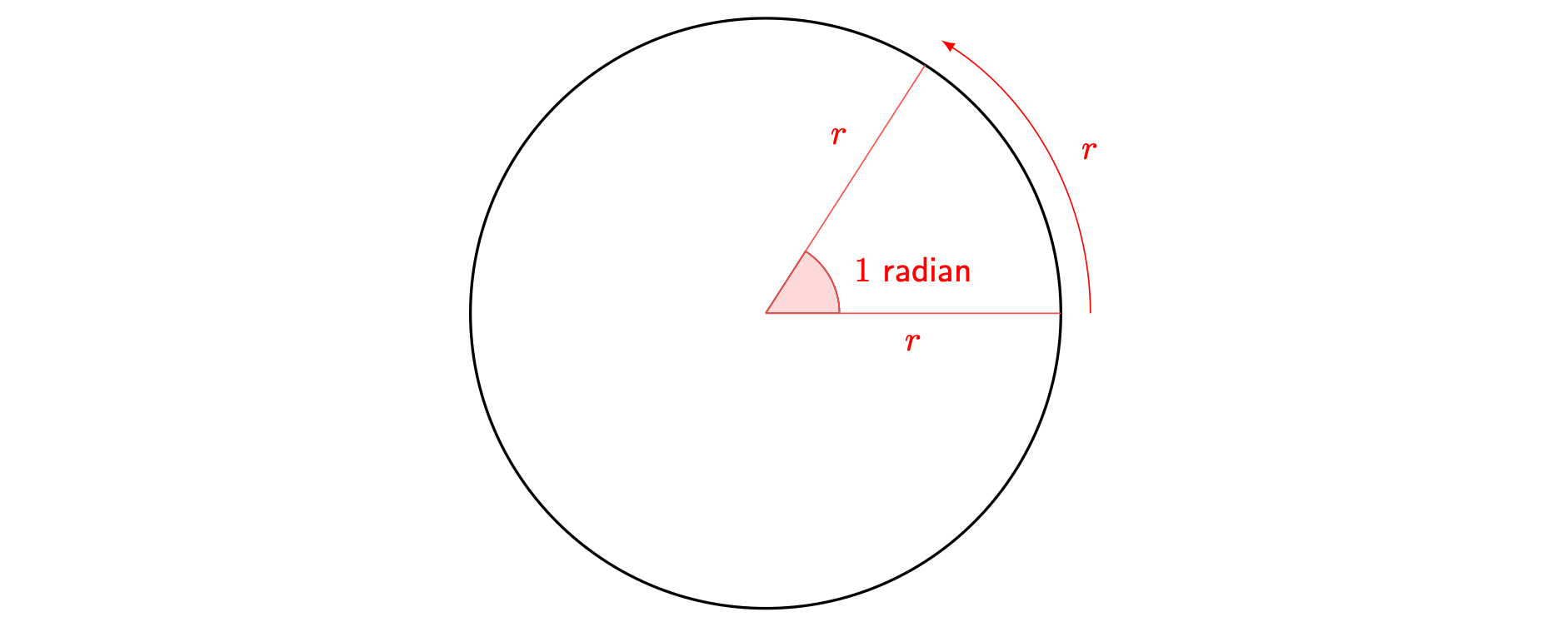
Pick any two points on a circle such that the length of the arc between them is equal to the radius of the circle and draw radiuses from these points to the centre. The angle between these two lines at the centre is defined to be \(1\) radian. A precise way to say this is:
One radian is the angle formed by the section of circle where the length of the arc \(a\) is the radius \(r\). See Figure 3 for a picture of this.
More generally, the angle \(\theta\) in radians is defined by \(a/r\), where \(a\) is the length of the arc and \(r\) is the radius of the circle.
You can notice that the size of the circle does not change the value of \(1\) rad - it is the same in any circle.
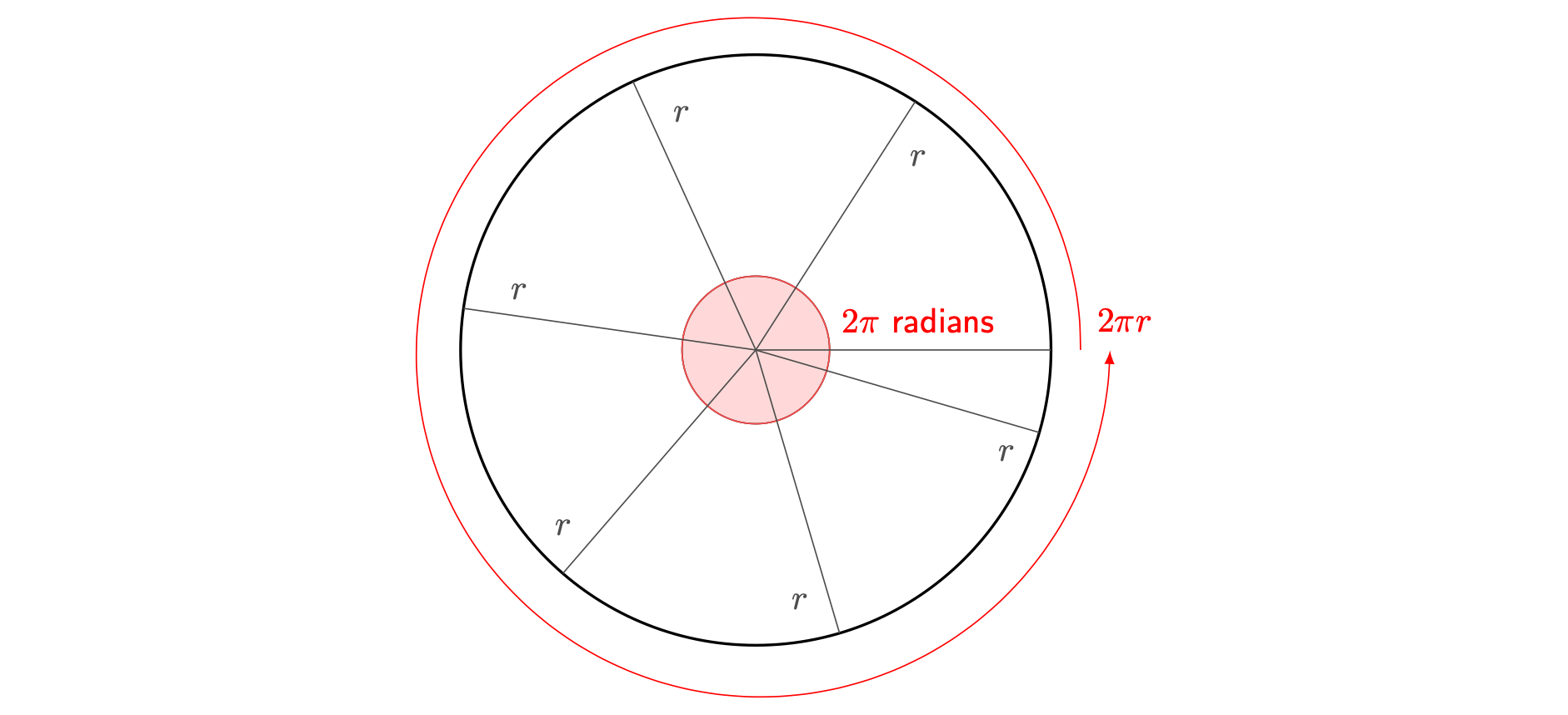
Using this definition, you can find the number of radians in a full circle. The well-known equation \(c = 2 \pi r\), where \(c\) is the circumference of a circle and \(r\) the radius, tells you that you can fit sectors with arc length \(r\) side by side into the circle \(2\pi\) times. Since each of these sectors has an angle of \(1\) radians at the centre, it follows that there are \(2\pi\) radians in the whole circle.
Converting between radians and degrees
The process for converting from radians to degrees and from degrees to radians are direct opposites to each other.
Converting from degrees to radians
Starting from an angle in degrees:
- Multiply the angle in degrees by \(\pi\)
- Divide the result by \(180\)
Your angle is now in radians.
More precisely, suppose you have an angle of \(x\) degrees. Then your angle in radians is equal to \(x\pi/180\). In particular, one degree is equal to \(\pi/180\) radians.
Where possible, remember to simplify fractions at the very end of your working.
You are given the angle \(180^\circ\) to convert to radians.
- Multiplying by \(\pi\) gives \(180\pi\)
- Dividing by 180 gives \(\pi\)
This means that \(180^\circ\) is equal to \(\pi\) rad.
Alternatively, you could put \(x = 180\) into the formula \(x\pi/180\) to obtain \(180\pi/180 = \pi\) as the angle in radians.
You are given the angle \(45^\circ\) to convert to radians.
- Multiplying by \(\pi\) gives \(45\pi\)
- Dividing by 180 gives \(\frac{\pi}{4}\)
This means that \(45^\circ\) is equal to \(\frac{\pi}{4}\) rad.
Alternatively, you could put \(x = 45\) into the formula \(x\pi/180\) to obtain \(45\pi/180 = \pi/4\) as the angle in radians.
You can notice that angles in radians are typically given as fractions of \(\pi\), rather than decimal numbers. In mathematics, it is usually better to express your answer exactly rather than as a decimal approximation.
Converting from radians to degrees
Starting from an angle in radians:
- Multiply the angle in radians by \(180\)
- Divide the result by \(\pi\)
Your angle is now in degrees.
More precisely, suppose you have an angle of \(y\) radians. Then your angle in degrees is equal to \(180y/\pi\). In particular, one radian is equal to \(180/\pi = 57.295\) degrees (to three decimal places).
You are given the angle \(5\pi/4\) rad to convert to degrees.
- Multiplying by \(180\) gives \(900\pi/4 = 225\pi\)
- Dividing the result by \(\pi\) gives \(225\).
This means that \(5\pi/4\) rad is equal to \(225^\circ\).
Alternatively, you could put \(y = 5\pi/4\) into the formula \(180y/\pi\) to obtain \(900\pi/4\pi = 225\) as the angle in degrees.
You are given the angle \(\frac{\pi}{6}\) rad to convert to degrees
- Multiplying by \(180\) gives \(180\pi/6 = 30\pi\)
- Dividing the result by \(\pi\) gives \(30\).
This means that \(\frac{\pi}{6}\) rad is equal to \(30^\circ\).
Alternatively, you could put \(y = \pi/6\) into the formula \(180y/\pi\) to obtain \(180\pi/6\pi = 30\) as the angle in degrees.
Useful conversions to know
Here is a table of useful conversions of degrees to radians that come up often:
| Angle in degrees | \(0\) | \(30\) | \(45\) | \(60\) | \(90\) | \(120\) | \(135\) | \(150\) | \(180\) | \(270\) | \(360\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle in radians | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(2\pi\) |
Arc length and sector area
If you have two radiuses of the circle and know the angle, in radians, between these radiuses, then you can calculate the length of the arc between these lines.
The length \(s\) of an arc between two points is given by \(s = r \theta\), where \(r\) is the radius of the circle and \(\theta\) is the angle, in radians, between the radiuses of the two given points.
To see why this equation holds, convince yourself that this equality is true (\(c\) is the circumference of the circle): \[\frac{s}{c} = \frac{\theta}{2\pi}.\] If you substitute \(c = 2\pi r\) into this equality, you get \[\frac{s}{2\pi r} = \frac{\theta}{2\pi}.\] Finally, rearranging gives you the equation \[s = r \theta.\]
Similar to arc length, you can get an equation in terms of radians to calculate the area of a sector.
The area \(A\) of a sector of a circle with radius \(r\) and angle \(\theta\) at the centre (in radians) is given by \(A = \frac{1}{2}r^2\theta\).
You are given a circle with radius \(4\). Find the length of arc and the area of the sector covering an angle of \(2\pi/3\) radians.
Using the formula for length of arc with \(r = 4\) and \(\theta = 2\pi/3\) gives \[s = 4\cdot \frac{2\pi}{3} = \frac{8\pi}{3}.\] Similarly, using the formula for area of the sector with \(r=4\) and \(\theta = 2\pi/3\) gives \[A = \frac{1}{2}\cdot\frac{4^2\cdot 2\pi}{3} = \frac{32\pi}{6} = \frac{16\pi}{3}.\]
Quick check problems
- You are given three degree to radians conversions. Determine whether they are true or false.
\(15^\circ = \dfrac{\pi}{12}\textsf{ rad}\) Answer: .
\(450^\circ = \dfrac{5\pi}{2}\textsf{ rad}\) Answer: .
\(720^\circ = 2\pi\textsf{ rad}\) Answer: .
- You are given three radians to degrees conversions. Determine whether they are true or false.
\(\dfrac{\pi}{24} \textsf{ rad} = 10\) Answer: .
\(3\pi \textsf{ rad} = 540\) Answer: .
\(\dfrac{3\pi}{4} \textsf{ rad} = 140\) Answer: .
- By entering your answer as a rational number \(a/b\) in its simplest terms, what fraction of \(\pi\) describes the following:
length of arc of circle with radius \(3\) over an angle of \(5\pi/6\) radians. Answer: .
area of sector of circle with radius \(2\) over an angle of \(\pi/4\) radians. Answer: .
Further reading
For more questions on the subject, please go to Questions: Radians.
To see how trigonometry interacts with radians as a measure of an angle, see Guide: Trigonometry (radians) and Guide: Trigonometric identities (radians).
Version history and licensing
v1.0: initial version created 08/23 by Ifan Howells-Baines and Mark Toner as part of a University of St Andrews STEP project.
- v1.1: edited 04/24 by tdhc.