Introduction to complex numbers
| Narration of study guide: |
What is a complex number?
Real numbers, which consist of all possible decimal numbers, can do lots of things very well. For instance, you can measure all possible lengths using real numbers, which you cannot do using rational numbers \(a/b\) with \(a,b\) whole numbers and \(b\) non-zero. You can also solve any equation \(ax = b\) for \(x\), with \(a,b\) non-zero real numbers.
But real numbers cannot do everything. Consider the equation \[x^2 = -1.\] Since the square of any real number is greater than or equal to \(0\), it follows that this equation has no solutions which are real numbers. So you will have to look elsewhere for the solution to such an equation; perhaps defining a new kind of number. Setting \(i\) to be a number such that \(i^2 = -1\) solves this issue; this \(i\) is known as the imaginary unit.
It turns out that introducing this imaginary unit \(i\) is enough to express solutions to all equations involving an \(x^2\) term, known as quadratic equations; for more on these, see Guide: Introduction to quadratic equations. By using this imaginary unit as the basis for a new number system containing the real numbers, you can solve all possible quadratic equations. This number system is known as the complex numbers.
Complex numbers appear almost everywhere in mathematics. Aside from being used to solve any quadratic equation, they have important applications in the theory of numbers more generally, in higher forms of algebra, the study of functions, the theory of electromagnetism, solving differential equations, and even measuring the motion of tornadoes!
This guide will focus on introducing the concept of a complex number, with the exact definition of complex numbers together with some initial examples of complex numbers. Then, the concepts of real and imaginary parts of complex numbers are explored, the complex conjugate is defined, and the pictorial representation of a complex number via Argand diagrams is explained.
Initial definitions of complex numbers
The key concept that separates complex numbers from real numbers is the existence of the imaginary unit, otherwise known as \(i\);
The imaginary unit \(i\) is defined by the fact that \(i^2 = -1\).
Sometimes the imaginary unit is written by \(j\) instead of \(i\). This is often used in contexts where \(i\) means something else, such as in engineering and in the programming language Python.
Now, you can use the imaginary unit to define a complex number:
Any number \(z = a + bi\) where \(a\) and \(b\) are real numbers is called a complex number.
The set of all complex numbers is called \(\mathbb{C}\).
Sometimes a complex number \(z = a + bi\) can be written as \(z = a + ib\). This particularly happens when \(b\) is a square root such as \(\sqrt{5}\), or the output of a function such as \(\sin(x)\).
Here are some complex numbers: \(z_1 = 1 + 3i\), \(z_2 = -4 + 6i\), \(z_3 = 8/3 - 13i/5\), \(z_4 = -\pi - i\pi\). Some more complex numbers are \(z_5 = 0 + 4i = 4i\) and \(z_6 = - 2 + 0i = -2\).
You can notice that in Example 1, \(z_5\) and \(z_6\) have \(a = 0\) and \(b = 0\) respectively. These are examples of some special kinds of complex numbers:
If \(b = 0\), then \(z = a\) is known as real number. So every real number is also a complex number.
If \(a = 0\), then \(z = bi\) is known as a purely imaginary number.
Square roots of negative numbers
You will notice that \(i\) is defined by the fact that \(i^2 = -1\). It is very important to say that \(i\) is not the only solution to the equation \(x^2 = -1\). Considering \((-i)^2\) and using the laws of indices (see Guide: Laws of indices) gives \[(-i)^2 = (-1\cdot i)^2 = (-1)^2\cdot i^2 = 1\cdot (-1) = -1\] and so \(-i\) is also a solution to \(x^2 = -1\).
Purely imaginary numbers are used to express solutions to the equation \(x^2 = -a\), where \(a > 0\) is a positive real number.
Let \(a > 0\) be a positive real number. Then the solutions to \(x^2 = -a\) are given by \[x = i\sqrt{a}\qquad\textsf{ and }x = -i\sqrt{a}.\]
The two solutions of \(x^2 = -64\) are \(x = 8i\) and \(x = -8i\).
The two solutions of \(x^2 = -3\) are \(x = i\sqrt{3}\) and \(x = -i\sqrt{3}\).
Real and imaginary parts
The real numbers \(a,b\) that form the two separate parts of the complex number \(z = a + bi\) have special names. These real numbers can be recovered from the complex number by taking real and imaginary parts:
If \(z = a + bi\) is a complex number, then:
the real part \(\textsf{Re}(z)\) of \(z\) is defined to be \(\textsf{Re}(z) = a\),
the imaginary part \(\textsf{Im}(z)\) of \(z\) is defined to be \(\textsf{Im}(z) = b\), the coefficient of \(i\) in \(z = a + bi\).
Sometimes, the real part of a complex number is written as \(\Re(z)\), and the imaginary part as \(\Im(z)\).
The real and imaginary parts of a complex number \(z = a + bi\) are real numbers, so your answer should not involve the imaginary unit.
In this language, a complex number \(z\) is real if and only if \(\textsf{Im}(z) = 0\); a complex number \(z\) is purely imaginary if and only if \(\textsf{Re}(z) = 0\).
In Example 1, you saw six complex numbers \(z_1\) to \(z_6\). Here, their real and imaginary parts are given.
The real part of \(z_1 = 1 + 3i\) is \(\textsf{Re}(z_1) = 1\), and the imaginary part of \(z_1\) is \(\textsf{Im}(z_1) = 3\).
The real part of \(z_2 = -4 + 6i\) is \(\textsf{Re}(z_2) = -4\), and the imaginary part of \(z_2\) is \(\textsf{Im}(z_2) = 6\).
The real part of \(z_3 = 8/3 - 13i/5\) is \(\textsf{Re}(z_3) = 8/3\), and the imaginary part of \(z_3\) is \(\textsf{Im}(z_3) = -13/5\).
The real part of \(z_4 = -\pi - i\pi\) is \(\textsf{Re}(z_4) = -\pi\), and the imaginary part of \(z_4\) is \(\textsf{Im}(z_4) = -\pi\).
The real part of \(z_5 = 4i\) is \(\textsf{Re}(z_5) = 0\), as \(z_5 = 4i = 0 + 4i\). The imaginary part of \(z_5\) is \(\textsf{Im}(z_5) = 4\).
The real part of \(z_6 = -2\) is \(\textsf{Re}(z_6) = -2\). The imaginary part of \(z_6\) is \(\textsf{Im}(z_6) = 0\), as \(z_6 = -2 = -2 + 0i\).
The complex conjugate
You saw in the previous section on square roots of negative numbers that the solutions to \(-a^2\) are \(i\sqrt{a}\) and \(-i\sqrt{a}\), where \(a\) is a positive number. As it turns out, this is an example of a more general phenomenon known as the complex conjugate.
If \(z = a + bi\) is a complex number, then the complex conjugate \(\bar{z}\) (or \(z^*\)) of \(z\) is the complex number \(\bar{z} = a - bi\).
So the complex conjugate of \(z = a + bi\) is the complex number with the same real part and with the sign of the imaginary part switched from either plus to minus or from minus to plus. Let’s take a look at some examples.
In Example 1, you saw six complex numbers \(z_1\) to \(z_6\). Here, their complex conjugates are given.
The complex conjugate of \(z_1 = 1 + 3i\) is \(\bar{z}_1 = 1 - 3i\).
The complex conjugate of \(z_2 = -4 + 6i\) is \(\bar{z}_2 = -4 - 6i\).
The complex conjugate of \(z_3 = 8/3 - 13i/5\) is \(\bar{z}_3 = 8/3 + 13i/5\).
The complex conjugate of \(z_4 = -\pi - i\pi\) is \(\bar{z}_4 = -\pi + i\pi\).
The complex conjugate of \(z_5 = 4i\) is \(\bar{z}_5 = -4i\).
The complex conjugate of \(z_6 = -2\) is \(\bar{z}_6 = -2\). Notice that taking the complex conjugate of any real number gives that same real number again!
You can see from Examples 2 and 3 (and the definition of complex conjugate) that if \(\textsf{Re}(z) = a\) then \(\textsf{Re}(\bar{z}) = a\), and if \(\textsf{Im}(z) = b\) then \(\textsf{Im}(\bar{z}) = -b\).
Argand diagrams
Because every complex number is writable as \(a + bi\) for \(a,b\in \mathbb{R}\), you can express every complex number \(a+bi\) as a point \((a,b)\) in two-dimensional space. Such a graph is known as an Argand diagram.
An Argand diagram has two axes called the real and imaginary axes. The real axis takes the place of the \(x\)-axis and the imaginary axis takes the place of the \(y\)-axis. See Figure 1 for more.
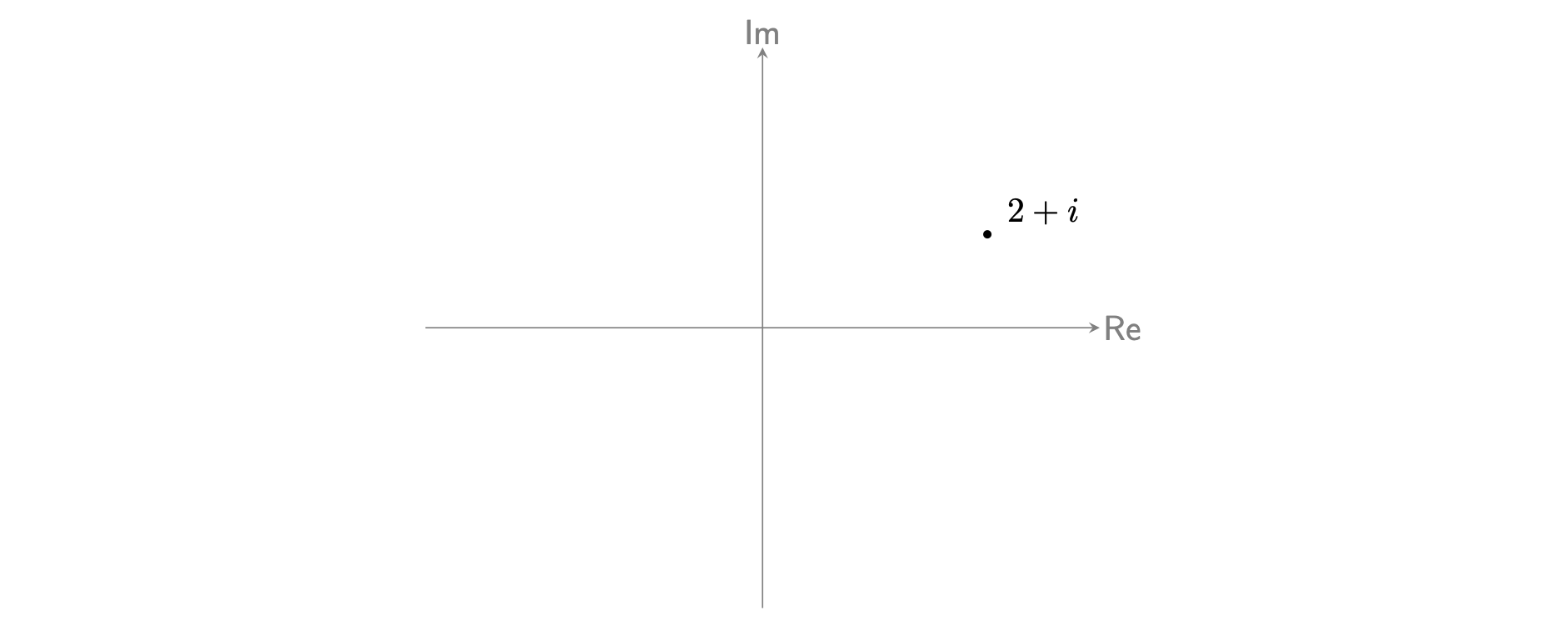
To draw a complex number on an Argand diagram, you can plot the complex number \(z = a + bi\) at the point \((a,b) = (\mathsf{Re}(z), \mathsf{Im}(z))\). See Figure 2 for a representation of \(z = 2 + i\) on an Argand diagram.
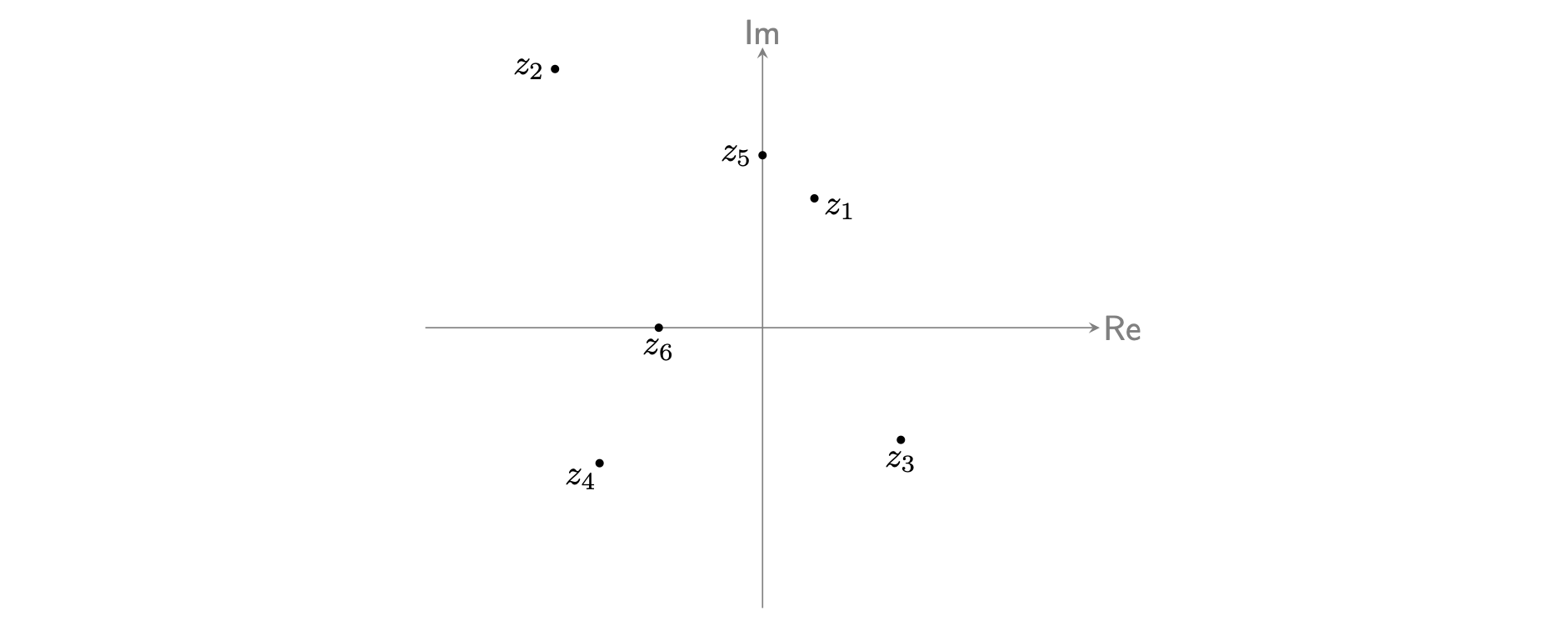
In Example 1, you saw six complex numbers \(z_1\) to \(z_6\), and Example 3 demonstrated the real and imaginary parts of these.
The real part of \(z_1 = 1 + 3i\) is \(\textsf{Re}(z_1) = 1\), and the imaginary part of \(z_1\) is \(\textsf{Im}(z_1) = 3\), so this corresponds to the point \((1,3)\).
The real part of \(z_2 = -4 + 6i\) is \(\textsf{Re}(z_2) = -4\), and the imaginary part of \(z_2\) is \(\textsf{Im}(z_2) = 6\). This corresponds to the point \((-4,6)\).
The real part of \(z_3 = 8/3 - 13i/5\) is \(\textsf{Re}(z_3) = 8/3\), and the imaginary part of \(z_3\) is \(\textsf{Im}(z_3) = -13/5\). This corresponds to the point \((8/3,-13/5)\) on the plane.
The real part of \(z_4 = -\pi - i\pi\) is \(\textsf{Re}(z_4) = -\pi\), and the imaginary part of \(z_4\) is \(\textsf{Im}(z_4) = -\pi\). This corresponds to the point \((-\pi,-\pi)\).
The real part of \(z_5 = 4i\) is \(\textsf{Re}(z_5) = 0\), as \(z_5 = 4i = 0 + 4i\). The imaginary part of \(z_5\) is \(\textsf{Im}(z_5) = 4\). This corresponds to a point \((0,4)\), on the \(y\)-axis.
The real part of \(z_6 = -2\) is \(\textsf{Re}(z_6) = -2\). The imaginary part of \(z_6\) is \(\textsf{Im}(z_6) = 0\), as \(z_6 = -2 = -2 + 0i\). This corresponds to \((2,0)\) on the \(x\)-axis.
See Figure 3 for an Argand diagram.
Quick check problems
- Give the real and imaginary parts of the following complex numbers: \(w_1 = 3+6i\), \(w_2 = -5 - 6i\), \(w_3 = 8 - i\), \(w_4 = 0\), and \(w_5 = x + 5i\).
Answers:
\(\textsf{Re}(w_1) =\) and \(\textsf{Im}(w_1) =\) .
\(\textsf{Re}(w_2) =\) and \(\textsf{Im}(w_2) =\) .
\(\textsf{Re}(w_3) =\) and \(\textsf{Im}(w_3) =\) .
\(\textsf{Re}(w_4) =\) and \(\textsf{Im}(w_4) =\) .
\(\textsf{Re}(w_5) =\) and \(\textsf{Im}(w_5) =\) .
- You are given three statements below. Decide whether they are true or false.
The complex conjugate of any purely imaginary number is a real number. Answer: .
The complex conjugate of \(a - bi\) is \(a + bi\) for all real numbers \(a,b\). Answer: .
Any real number is also a complex number. Answer: .
Further reading
For more questions on the subject, please go to Questions: Introduction to complex numbers.
Version history
v1.0: initial version created 10/24 by tdhc.