Vector addition and scalar multiplication

Geometry

Vectors

Linear mathematics

Author

Renee Knapp, Kin Wang Pang

Summary

Understanding and utilising vector addition and scalar multiplication are essential when studying vectors, particularly when it comes to solving equations involving vectors.

Before reading this guide, it is recommended that you read Guide: Introduction to vectors.

What is vector addition and scalar multiplication?

As you have seen in Guide: Introdution to vectors, vectors have a magnitude and a direction and are represented in coordinate spaces by components, either in $\mathbf{i},\mathbf{j},\mathbf{k}$ notation or as a column vector. These components can be considered independent to each other.

You are able to add two vectors together, or multiply a vector by a scalar. To do this, you have to consider each component of the vector individually. These ideas of vector addition and scalar multiplication are key concepts in linear mathematics, which underpins many important concepts in applied mathematics, physics, chemistry, statistics, economics, and computer science – linear mathematics is even used in generative AI and machine learning!

This guide introduces vector addition and scalar multiplication, for vectors in both $\mathbf{i}$,$\mathbf{j}$,$\mathbf{k}$ and column notation, and explains the role of vector addition and scalar multiplication in solving equations using vectors.

Following the lead of Guide: Introduction to vectors this guide solely works on vectors in three dimensions.

Vector addition and subtraction

Definition and initial examples

The addition of vectors $\mathbf{u}$ and $\mathbf{v}$ is defined by following $\mathbf{u}$ and then $\mathbf{v}$. More specifically, you can join the start of a vector $\mathbf{v}$ to the end of another vector $\mathbf{u}$, and then draw a vector $\mathbf{u}+\mathbf{v}$ from the start of $\mathbf{u}$ to the end of $\mathbf{v}$. See Figure Figure 1 for a picture of this process.

(1) There are two vectors u and v. (2) The head of vector u is joined to the tail of vector v. (3) This forms a triangle and the new vector u + v is created by completing the triangle. This vector points from the tail of u to the head of v. — Figure 1: Graphical representation of vector addition. The three steps of the process are labelled.

What does this mean for a vector written in $\mathbf{i},\mathbf{j},\mathbf{k}$ notation? Examining the $\mathbf{i}$ component of the vector $\mathbf{u}+\mathbf{v}$, you can notice that you first move using $\mathbf{i}$ component of $\mathbf{u}$ and then move by the $\mathbf{i}$ component of $\mathbf{v}$. It follows that the $\mathbf{i}$ component of the vector $\mathbf{u}+\mathbf{v}$ is the sum of the $\mathbf{i}$ component of $\mathbf{u}$ and $\mathbf{i}$ component of $\mathbf{v}$. You can expand this to both the $\mathbf{j}$ and $\mathbf{k}$ components of $\mathbf{u}+\mathbf{v}$ to get the following definition.

Definition of vector addition

Let $\mathbf{a} = a_1 \mathbf{i} + a_2 \mathbf{j} + a_3 \mathbf{k}$ and $\mathbf{b} = b_1 \mathbf{i} + b_2 \mathbf{j} + b_3 \mathbf{k}$ be two vectors. Then the addition of the two vectors, written as $\mathbf{a} + \mathbf{b}$, is defined as follows: \[\mathbf{a} + \mathbf{b} = (a_1+b_1) \mathbf{i} + (a_2 + b_2) \mathbf{j} + (a_3 + b_3)\mathbf{k}.\] In column vector notation, the addition of $\mathbf{a} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ and $\mathbf{b} = \begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ is: \[\mathbf{a} + \mathbf{b} = \begin{pmatrix}a_1 + b_1\\a_2 + b_2\\a_3 + b_3\end{pmatrix}.\]

Example 1

You are given $\mathbf{a} = 3\mathbf{i} + 4\mathbf{j} - 8\mathbf{k}$ and $\mathbf{b} = 2\mathbf{i} +8\mathbf{j} + 12\mathbf{k}$. Then \[\begin{align*} \mathbf{a} + \mathbf{b} &= (3\mathbf{i} + 4\mathbf{j} - 8\mathbf{k}) + (2\mathbf{i} +8\mathbf{j} + 12\mathbf{k})\\ &=(3+2)\mathbf{i} + (4+8)\mathbf{j} + (-8 + 12)\mathbf{k}\\ &=5\mathbf{i} + 12\mathbf{j} + 4\mathbf{k} \end{align*}\]

Example 2

You are given $\mathbf{a} = \begin{pmatrix}3\\4\\-2\end{pmatrix}$ and $\mathbf{b} = \begin{pmatrix}5\\6\\14\end{pmatrix}$. Then \[\mathbf{a} + \mathbf{b} = \begin{pmatrix}3\\4\\-2\end{pmatrix} + \begin{pmatrix}5\\6\\14\end{pmatrix} = \begin{pmatrix}3+5\\4+6\\-2 + 14\end{pmatrix} = \begin{pmatrix}8\\10\\12\end{pmatrix}.\]

To subtract one vector from another, you can use the definition of a negative vector from Guide: Introduction to vectors. Much like for numbers, you can write that \[\mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}).\] So to subtract to vectors, you need to add $-\mathbf{v}$ to $\mathbf{u}$ using vector addition.

Geometrically, you need tp reverse the direction of the vector $\mathbf{v}$ first before finding $\mathbf{u} + (-\mathbf{v})$ in the usual fashion. Figure 2 explains this process.

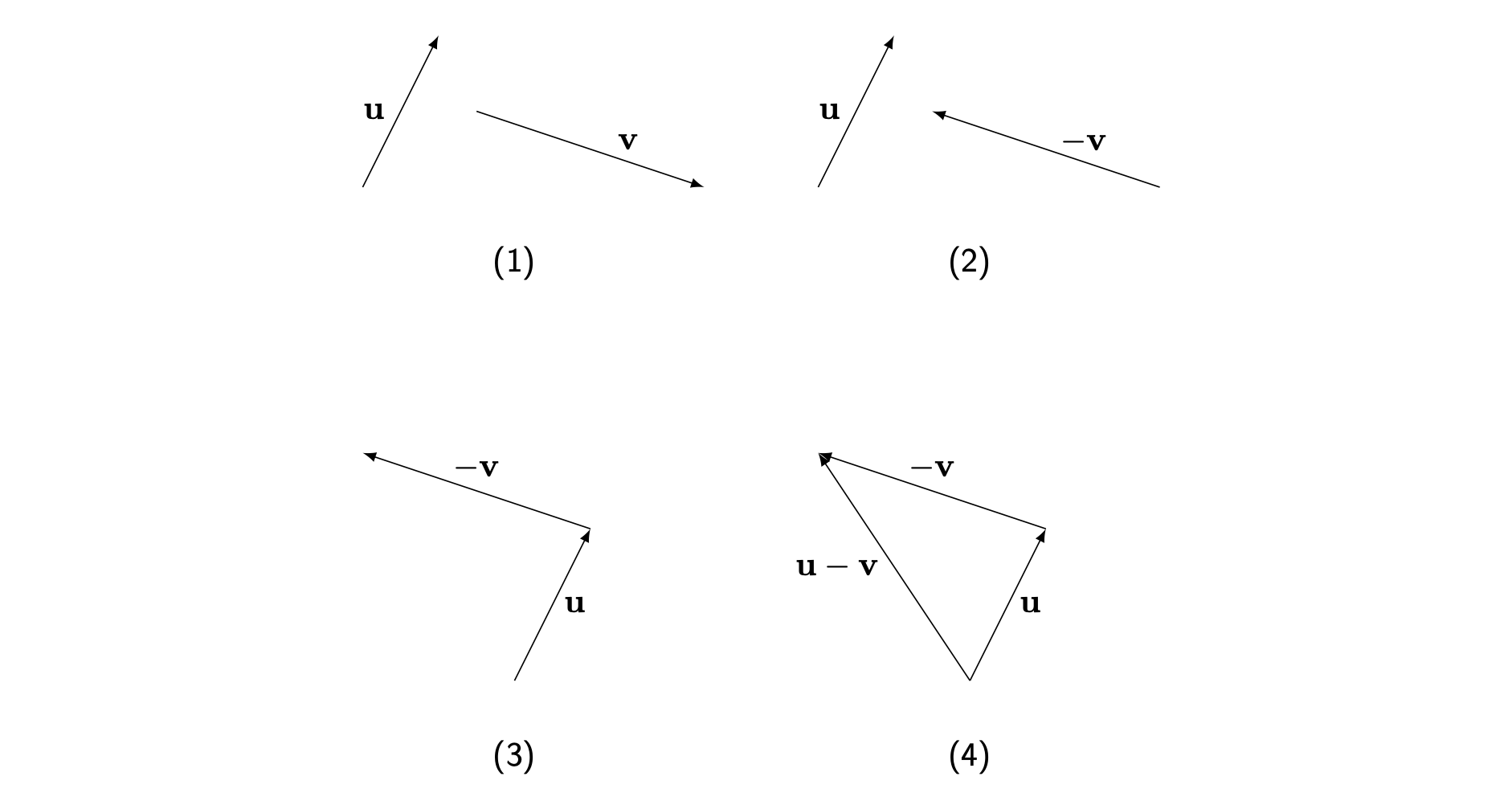
(1) There are two vectors u and v. (2) The direction of vector v is reversed in direction to form the negative v vector. (3) Then the head of vector u joins the tail of vector -v. (4) Completing the triangle gives the vector u - v. This vector points from the tail of u to the head of -v. — Figure 2: Graphical representation of vector subtraction. The four steps are labelled.

Example 3

You are given $\mathbf{a} = 3\mathbf{i} + 4\mathbf{j} + 3\mathbf{k}$ and $\mathbf{b} = 5\mathbf{i} - 6\mathbf{j}$. Then \[\begin{align*} \mathbf{a} - \mathbf{b} &= \mathbf{a} + (-\mathbf{b})\\ &= (3\mathbf{i} + 4\mathbf{j} + 3\mathbf{k}) + (-5\mathbf{i} + 6\mathbf{j})\\ &= (3-5)\mathbf{i} + (4+6)\mathbf{j} + (3 + 0)\mathbf{k}\\ &= -2\mathbf{i} + 10\mathbf{j} + 3\mathbf{k} \end{align*}\]

You can notice that you don’t need to work out $-\mathbf{b}$ or similar; notice that if $\mathbf{a} = a_1 \mathbf{i} + a_2 \mathbf{j} + a_3 \mathbf{k}$ and $\mathbf{b} = b_1 \mathbf{i} + b_2 \mathbf{j} + b_3 \mathbf{k}$, then \[\mathbf{a} - \mathbf{b} = (a_1-b_1) \mathbf{i} + (a_2 - b_2) \mathbf{j} + (a_3 - b_3)\mathbf{k}\] or, in column notation, \[\mathbf{a} - \mathbf{b} = \begin{pmatrix}a_1 - b_1\\a_2 - b_2\\a_3 - b_3\end{pmatrix}.\]

Warning

Be careful with your signs when subtracting vectors in this way!

Example 4

You are given $\mathbf{a} = \begin{pmatrix}3\\0\\-2\end{pmatrix}$ and $\mathbf{b} = \begin{pmatrix}5\\6\\-14\end{pmatrix}$. Then \[\mathbf{a} - \mathbf{b} = \begin{pmatrix}3\\0\\-2\end{pmatrix} - \begin{pmatrix}5\\6\\-14\end{pmatrix} = \begin{pmatrix}3-5\\0-6\\-2 - (-14)\end{pmatrix} = \begin{pmatrix}-2\\-6\\12\end{pmatrix}.\]

Properties of vector addition

The process of adding vectors via their components is called componentwise addition. The addition of the components is the same as adding numbers, so you may expect properties of adding numbers to be reflected in vector addition. In fact, the following properties are true for all vectors $\mathbf{u},\mathbf{v},\mathbf{w}$.

$\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}$ (called commutativity)
$(\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w})$ (called associativity).

The zero vector (see Guide: Introduction to vectors) plays an important role in properties of vector addition. In fact, there are two more properties relating entirely to the zero vector, which are true for all vectors $\mathbf{u}$:

$\mathbf{0} + \mathbf{u} = \mathbf{u}$
$\mathbf{u} + (-\mathbf{u}) = \mathbf{0}$

Example 5

You are given $\mathbf{a}= 2\mathbf{i}+ y\mathbf{j}-3\mathbf{k}$. Then \[\mathbf{a} + \mathbf{0} = (2+0)\mathbf{i}+ (y+0)\mathbf{j}+(-3+0)\mathbf{k} = 2\mathbf{i}+ y\mathbf{j}-3\mathbf{k} = \mathbf{a}\] (as you would expect!)

Example 6

You are given $\mathbf{a} = \begin{pmatrix}2\\1\\0\end{pmatrix}$, $\mathbf{b} = \begin{pmatrix}7\\2\\1\end{pmatrix}$ and $\mathbf{c} = \begin{pmatrix}-3\\-2\\5\end{pmatrix}.$

Then $\mathbf{a} + \mathbf{b} - \mathbf{c} = \begin{pmatrix}2+7 - (-3)\\1+2-(-2)\\0 + 1 - 5\end{pmatrix} = \begin{pmatrix}12\\5\\-4\end{pmatrix}$

Scalar multiplication

Definition and initial examples

As was mentioned in Guide: Introduction to vectors, another thing that you can do with vectors is to multiply it with a scalar, which is usually a real number. Scalar multiplying a vector by a positive scalar typically changes the magnitude of the vector and preserves the direction, and multiplying a vector by a negative scalar typically changes the magnitude of the vector and reverses the direction. Figure 3 shows a picture of these scenarios.

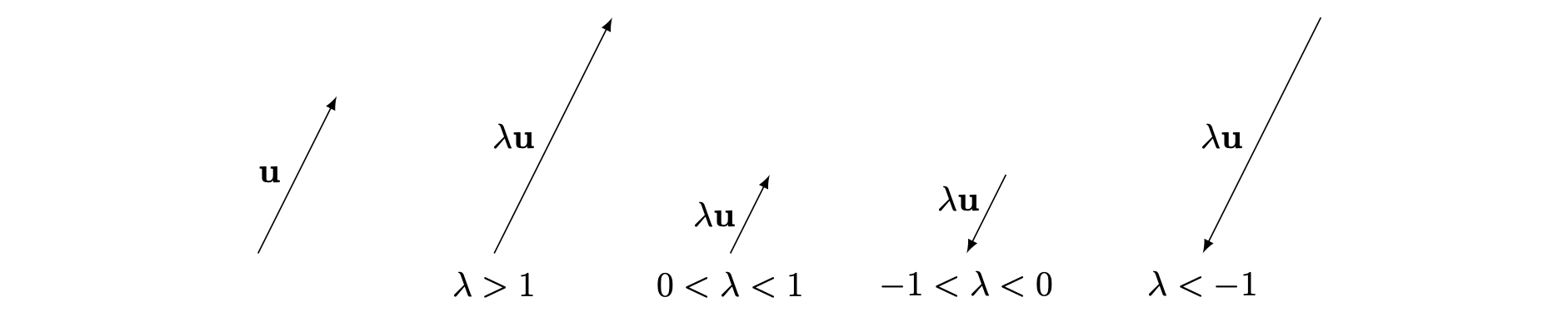
There are five vectors side by side. Going from left to right, the first shows the general vector u. The second shows the vector lambda u, where lambda is larger than one. The vector is lambda times longer than the vector u, pointing in the same direction. The third vector shows the vector lambda u, where lambda is between one and zero. The magnitude of the vector is shorter than the original vector u by a factor of 1/lambda. The fourth vector shows lambda u, where lambda is between negative one and zero. The magnitude of the vector is shorter than the original vector u by a factor of 1/lambda, and the direction of the vector is reversed. The fifth vector shows the vector lambda u, where lambda is smaller than negative one. The magnitude of the vector is longer than the original vector u by a factor of lambda, and direction of the vector is inverted. — Figure 3: Graphical representation of scalar multiplication.

What does scalar multiplication do to the components of a vector? Suppose that you are scalar multiplying the vector $\mathbf{i}$. This is a unit vector, so has magnitude $1$. Since scalar multiplication by a scalar $\lambda$ (pronounced ‘lambda’) changes the length of a vector, it follows that the vector $\lambda\mathbf{i}$ has magnitude $|\lambda|$, the absolute value of $\lambda$.

Since every vector $\mathbf{u}$ is the sum of scalar multiples of $\mathbf{i},\mathbf{j},\mathbf{k}$, it follows that $\lambda\mathbf{u}$ is the sum of scalar multiples of $\lambda\mathbf{i},\lambda\mathbf{j},\lambda\mathbf{k}$. This forms the basis of the definition:

Definition of scalar multiplication

Let $\mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} + a_3\mathbf{k}$ be a vector and let $\lambda$ be a real number. Then the scalar multiple of $\mathbf{a}$ by $\lambda$ is given by \[\lambda \mathbf{a} = \lambda a_1\mathbf{i} + \lambda a_2\mathbf{j} + \lambda a_3\mathbf{k}.\]

In column notation, if $\mathbf{a} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$, then $\lambda \mathbf{a} = \begin{pmatrix}\lambda a_1\\ \lambda a_2\\ \lambda a_3 \end{pmatrix}.$

Example 7

You are given $\mathbf{a} = \begin{pmatrix}3\\5\\6\end{pmatrix}$. Then $5\mathbf{a} = \begin{pmatrix}5(3)\\5(5)\\5(6)\end{pmatrix} = \begin{pmatrix}15\\25\\30\end{pmatrix}.$

Example 8

You are given $\mathbf{b} = -2\mathbf{i} + 6\mathbf{j} - 7\mathbf{k}$. Then \[-3\mathbf{b} = (-3)(-2)\mathbf{i} + (-3)6\mathbf{j} - (-3)7\mathbf{k} = 6\mathbf{i} -18\mathbf{j} + 21\mathbf{k}.\]

Properties of scalar multiplication

Since scalar multiplication is similar to component-wise multiplication, then it has the following properties for all vectors $\mathbf{u}$ and $\mathbf{v}$ and scalars $\lambda$ and $\mu$:

$(\lambda \mu) \mathbf{u} = \lambda (\mu \mathbf{u})$ (called associativity of scalar multiplication)
$( \lambda + \mu ) \mathbf{u} = \lambda \mathbf{u} + \mu \mathbf{u}$ (called distributivity of scalar multiplication)
$\lambda (\mathbf{u} + \mathbf{v}) = \lambda\mathbf{u} + \lambda\mathbf{v}$ (called distributivity of vector addition)
$1\mathbf{u} = \mathbf{u}$ (so $1$ is the scalar multiplicative identity)

In addition, the following are also true:

$0\mathbf{u} = \mathbf{0}$, so any vector scalar multiplied by $0$ gives the zero vector $\mathbf{0}$.
$(-1)\mathbf{u} = -\mathbf{u}$

Finally, if two vectors are scalar multiples of each other, then they must have either the same direction or exactly opposite directions.

Tip

If $\mathbf{u}$ and $\mathbf{v}$ are general vectors such that $\mathbf{u} = \lambda \mathbf{v}$ for some positive scalar $\lambda$, then $\mathbf{u}$ and $\mathbf{v}$ are parallel to each other. If $\mathbf{u} = \lambda \mathbf{v}$ for some negative scalar $\lambda$, then $\mathbf{u}$ and $\mathbf{v}$ are antiparallel to each other.

Equivalently, two vectors $\mathbf{u}$ and $\mathbf{v}$ are parallel if their correpsonding unit vectors are equal; so when $\hat{\mathbf{u}} = \hat{\mathbf{v}}$. You can say that $\mathbf{u}$ and $\mathbf{v}$ are antiparallel if $\hat{\mathbf{u}} = -\hat{\mathbf{v}}$.

Solving vector equations

By combining addition and scalar multiplication, you can form vector equations. It is extremely important to be able to solve vector equations. They have many applications in varied field such as geometry, mechanics, multivariable calculus and more. In addition, solving vector equations is one of the key studies of linear mathematics.

One thing to remember from Guide: Introduction to vectors is that vectors are only equal if and only if their components are individually equal. That is, if $\mathbf{a} = a_1 \mathbf{i} + a_2 \mathbf{j} + a_3 \mathbf{k}$ and $\mathbf{b} = b_1 \mathbf{i} + b_2 \mathbf{j} + b_3 \mathbf{k}$ are two vectors, then \[\mathbf{a} = \mathbf{b}\quad\textsf{ if and only if }\quad a_1 = b_1,\, a_2 = b_2,\, a_3 = b_3.\]

This means that to solve vector equations, you may have to solve three equations simultaneously! This requires an excellent knowledge of solving simultaneous equations; see [Guide: Solving simultaneous equations] for more.

Solving vector equations is best done when following the lead of examples; here are two. The first of these involves position vectors: see Guide: Introduction to vectors for more.

Example 9

If the co-ordinates of the point $B$ are $(-5,-2,-4)$ and $\overrightarrow{AB} = \begin{pmatrix}1\\1\\-6\end{pmatrix}$, what are the co-ordinates of $A$?

Using knowledge from Guide: Introduction to vectors, you can say that the position vector of the point $B$ is \[\overrightarrow{OB} = \begin{pmatrix}-5\\-2\\-4\end{pmatrix}\]

If you can find the value of the position vector $\overrightarrow{OA}$, then you can read off the co-ordinates of the point $A$. Using the definition of vector addition, you can write that \[\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}\] and so $\overrightarrow{OA} = \overrightarrow{OB} - \overrightarrow{AB}$. Therefore \[\overrightarrow{OA} = \overrightarrow{OB} - \overrightarrow{AB}= \begin{pmatrix}-5\\-2\\-4\end{pmatrix} - \begin{pmatrix}1\\1\\-6\end{pmatrix} = \begin{pmatrix}-6\\-3\\2\end{pmatrix}\] and so the co-ordinates of $A$ are $(-6,-3,2)$.

Example 10

If $\mathbf{u} = 4\mathbf{i} + 3\mathbf{j}$ and $\mathbf{v} = -\mathbf{i} + 2\mathbf{j}$, how can you express $7\mathbf{i} + 19\mathbf{j}$ in terms of $\mathbf{u}$ and $\mathbf{v}$?

What you can do here is take the sum of scalar multiples of $\mathbf{u}$ and $\mathbf{v}$ (known as a linear combination) and set this vector equal to $7\mathbf{i} + 19 \mathbf{j}$. It is important that you take these two scalars to be potentially different, so give them different names like $\lambda$ (‘lambda’) and $\mu$ (‘mu’). So \[7\mathbf{i} + 19 \mathbf{j} = \lambda \mathbf{u} + \mu \mathbf{v}\] Since $\mathbf{u} = 4\mathbf{i} + 3\mathbf{j}$ and $\mathbf{v} = -\mathbf{i} + 2\mathbf{j}$, this becomes \[7\mathbf{i} + 19 \mathbf{j} = (4\lambda \mathbf{i} + 3\lambda\mathbf{j}) + (-\mu\mathbf{i} + 2\mu\mathbf{j})\] These two vectors are equal if and only if their components are equal. Therefore, this gives two simultaneous equations \[\begin{align*} 7 &= 4\lambda - \mu \tag{\textsf{$\mathbf{i}$ component}}\\ 19 &= 3\lambda + 2\mu \tag{\textsf{$\mathbf{j}$ component}} \end{align*}\] Solving these equations (see [Guide: Solving simultaneous equations] for more) gives $\lambda = 3$ and $\mu = 5$, and so \[7\mathbf{i} + 19\mathbf{j} = 3\mathbf{u} + 5\mathbf{v}.\]

Quick check problems

If $\mathbf{a} = \begin{pmatrix}0\\-6\\2\end{pmatrix}$, then what is $7\mathbf{a}$?

Answer: $7\mathbf{a}$ is equal to $\mathbf{i}$ + $\mathbf{j}$ + $\mathbf{k}$.

If $\mathbf{b} = 2\mathbf{i} + 6\mathbf{k}$ and $\mathbf{c} = -5\mathbf{i} + 3\mathbf{j} + 2\mathbf{k}$, then what is $\mathbf{c} + 2\mathbf{b}$?

Answer: $\mathbf{c} + 2\mathbf{b}$ = $\mathbf{i}$ + $\mathbf{j}$ + $\mathbf{k}$.

Given that the coordinates $A = \begin{pmatrix}2\\-1\\4\end{pmatrix}$ and $B = \begin{pmatrix}3\\-3\\-6\end{pmatrix}$, what is the vector $\overrightarrow{AB}$?

Answer: $\mathbf{i}$ + $\mathbf{j}$ + $\mathbf{k}$.

You are given three statements below. Decide whether they are true or false.

If $\overrightarrow{AB} = 2\mathbf{BC}$, the two vectors are perpendicular. Answer: .
If $12\mathbf{a} - 4\mathbf{b} = 8\mathbf{c}$, then $2\mathbf{c} + \mathbf{b} = 3\mathbf{a}$. Answer: .
If $\lambda \mathbf{a} + \mu \mathbf{b} = \mathbf{0}$ and $\mathbf{a}$ and $\mathbf{b}$ are parallel non-zero vectors, then $\lambda = \mu = 0$ is the only solution to this vector equation. Answer: .

Vector addition and scalar multiplication

What is vector addition and scalar multiplication?

Vector addition and subtraction

Definition and initial examples

Properties of vector addition

Scalar multiplication

Definition and initial examples

Properties of scalar multiplication

Solving vector equations

Quick check problems

Further reading

Version history and licensing

Feedback