Answers: Introduction to complex numbers
These are the answers to Questions: Introduction to complex numbers.
Please attempt the questions before reading these answers!
Q1
Using complex numbers, find solutions to the following equations.
1.1. Here, \(x = i\) and \(x = -i\) are the two solutions.
1.2. Here, \(x = 3i\) and \(x = -3i\) are the two solutions.
1.3. Here, \(x = 12i\) and \(x = -12i\) are the two solutions.
1.4. Here, \(x = 1\) and \(x = -1\) are the two solutions. (Real numbers are complex numbers too!)
Q2
For each of the complex numbers below, give their real and imaginary parts. (In this question, \(a,b\) are real numbers.)
2.1. The real part of \(z_1\) is \(\textsf{Re}(z_1) = 2\) and the imaginary part of \(z_1\) is \(\textsf{Im}(z_1) = 3\).
2.2. The real part of \(z_2\) is \(\textsf{Re}(z_2) = -23\) and the imaginary part of \(z_2\) is \(\textsf{Im}(z_2) = 32\).
2.3. The real part of \(z_3\) is \(\textsf{Re}(z_3) = 3\) and the imaginary part of \(z_3\) is \(\textsf{Im}(z_3) = -3\).
2.4. The real part of \(z_4\) is \(\textsf{Re}(z_4) = 0\) and the imaginary part of \(z_4\) is \(\textsf{Im}(z_4) = 3\).
2.5. The real part of \(z_5\) is \(\textsf{Re}(z_5) = -3\) and the imaginary part of \(z_5\) is \(\textsf{Im}(z_5) = -2\).
2.6. The real part of \(z_6\) is \(\textsf{Re}(z_6) = a\) and the imaginary part of \(z_6\) is \(\textsf{Im}(z_6) = 2b\).
2.7. The real part of \(z_7\) is \(\textsf{Re}(z_7) = 2\) and the imaginary part of \(z_7\) is \(\textsf{Im}(z_7) = 0\).
2.8. The real part of \(z_8\) is \(\textsf{Re}(z_8) = 3/2\) and the imaginary part of \(z_8\) is \(\textsf{Im}(z_8) = 2/3\).
2.9. The real part of \(z_9\) is \(\textsf{Re}(z_9) = 22\) and the imaginary part of \(z_9\) is \(\textsf{Im}(z_9) = -33\).
2.10. The real part of \(z_{10}\) is \(\textsf{Re}(z_{10}) = 333\) and the imaginary part of \(z_{10}\) is \(\textsf{Im}(z_{10}) = 22\).
2.11. The real part of \(z_{11}\) is \(\textsf{Re}(z_{11}) = -2\) and the imaginary part of \(z_{11}\) is \(\textsf{Im}(z_{11}) = 2\).
2.12. The real part of \(z_{12}\) is \(\textsf{Re}(z_{12}) = -2\) and the imaginary part of \(z_{11}\) is \(\textsf{Im}(z_{11}) = -3\).
Q3
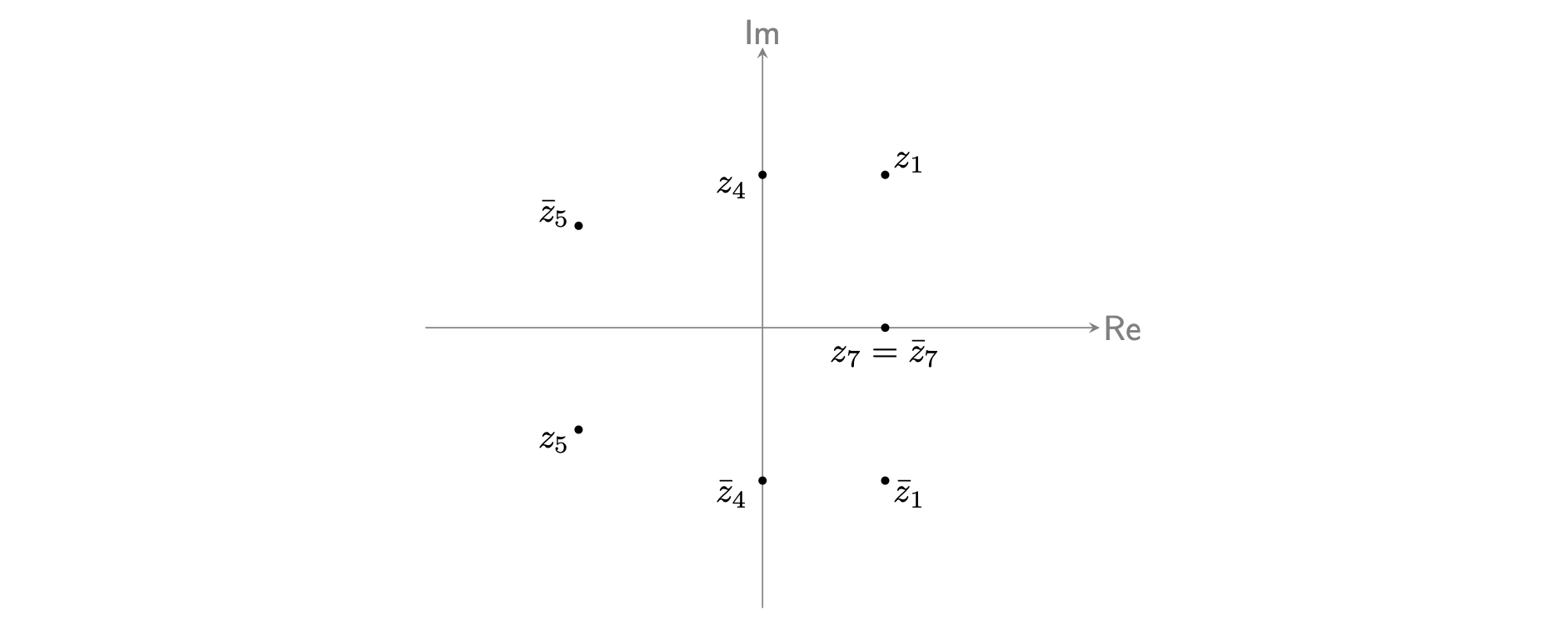
The complex conjugate of \(z_1 = 2 + 3i\) is \(\bar{z}_1 = 2-3i\).
The complex conjugate of \(z_2 = -23 + 32i\) is \(\bar{z}_2 = -23-32i\).
The complex conjugate of \(z_3 = 3 - 3i\) is \(\bar{z}_3 = 3+3i\).
The complex conjugate of \(z_4 = 3i\) is \(\bar{z}_4 = -3i\).
The complex conjugate of \(z_5 = - 3 - 2i\) is \(\bar{z}_5 = -3+2i\).
The complex conjugate of \(z_6 = a + 2bi\) is \(\bar{z}_6 = a-2bi\).
The complex conjugate of \(z_7 = 2\) is \(\bar{z}_7 = 2\).
The complex conjugate of \(z_8 = 3/2 + 2i/3\) is \(\bar{z}_8 = 3/2 - 2i/3\).
The complex conjugate of \(z_9 = 22 - 33i\) is \(\bar{z}_9 = 22 + 33i\).
The complex conjugate of \(z_{10} = 333 + 22i\) is \(\bar{z}_{10} = 333 + 22i\).
The complex conjugate of \(z_{11} = 2i - 2\) is \(\bar{z}_{11} = -2i - 2\).
The complex conjugate of \(z_{12} = -3i - 2\) is \(\bar{z}_{12} = 3i - 2\).
Q4
See Figure 1 for the Argand diagram. You can notice that the complex conjugates of the complex numbers can be obtained by reflecting the point in the real axis.
Version history and licensing
v1.0: initial version created 10/24 by tdhc.