Trigonometry (degrees)
Degrees are used throughout this guide. If you would like to see this guide using radians, please see Guide: Trigonometry (radians).
| Narration of study guide: |
What is trigonometry?
Trigonometry deals with the relationship between the angles and the sides of a triangle. It can be used to calculate the heights of buildings, construct planes and even in the motion of heroes in video games. This guide will look at defining the three standard trigonometric functions (sine (\(\sin\)), cosine (\(\cos\)), tangent (\(\tan\))), how to find the values of these functions from a given angle, some values to remember, and ending on the three remaining circular trigonometric functions (cosecant (\(\csc\)), secant (\(\sec\)), and cotangent (\(\cot\))).
Starting points
The first introduction you may have had to the trigonometric functions is in the context of right angled triangles. If you pick an angle you want to focus on, you can then label the side opposite it with ‘o’, the side which has no contact with the right angle ‘h’ (for hypotenuse), and the final side as ‘a’ (as it is adjacent to the angle)- see ?@fig-1.
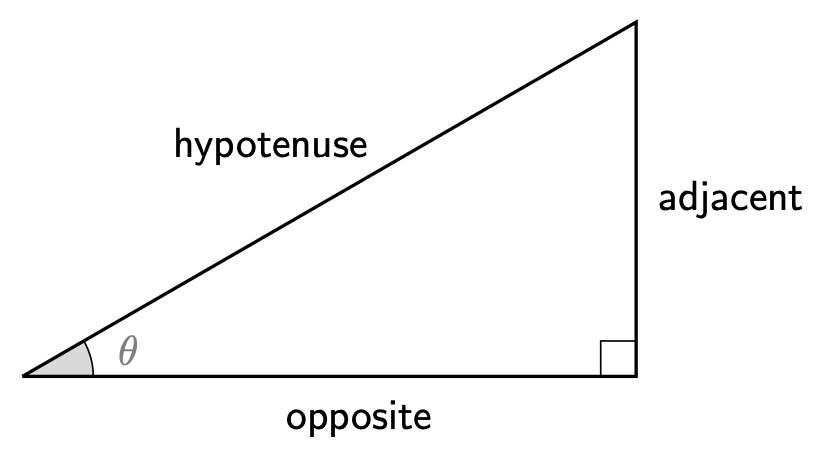 {width=“100%” fig-alt=“A right triangle labeled with its sides in relation to angle θ (theta), which is located at the bottom left corner. The side opposite angle θ is labeled”opposite,” the side next to angle θ and not the hypotenuse is labeled “adjacent,” and the longest side is labeled “hypotenuse.” The triangle includes a right angle in the bottom right corner.” #fig-1}
{width=“100%” fig-alt=“A right triangle labeled with its sides in relation to angle θ (theta), which is located at the bottom left corner. The side opposite angle θ is labeled”opposite,” the side next to angle θ and not the hypotenuse is labeled “adjacent,” and the longest side is labeled “hypotenuse.” The triangle includes a right angle in the bottom right corner.” #fig-1}
If you have some information about either two sides or a side and an angle, you can use the trigonometric functions to figure out the size of the angle or the other side.
The three main trigonometric functions \(\sin(\theta)\), \(\cos(\theta)\), and \(\tan(\theta)\) are defined with respect to ?@fig-1 in the following way:
\[\sin(\theta) = \frac{\textsf{opposite}}{\textsf{hypotenuse}} \qquad \cos(\theta) = \frac{\textsf{adjacent}}{\textsf{hypotenuse}}\qquad \tan(\theta) = \frac{\textsf{opposite}}{\textsf{adjacent}}\]
The abbreviation ‘SOH, CAH, TOA’ is often used to remember the definitions of the trigonometric functions. The first letter in each word represents the function, the second the numerator and the third the denominator. For example, SOH says that “you can find sin by dividing the opposite by the hypotenuse.”
You are given a triangle in Figure 1.
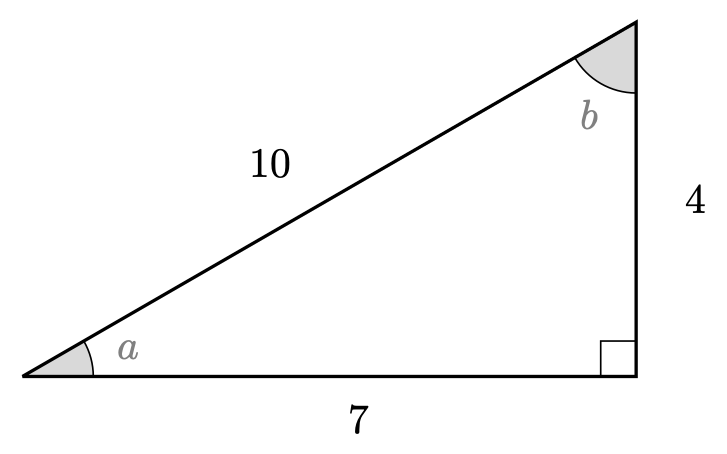
Find \(\cos(a)\), \(\sin(a)\), and \(\tan(b)\).
The adjacent side to the angle \(a\) has length \(7\), and the hypotenuse has length \(10\), so by the definition of \(\cos\) you can say that \[\cos(a) = \frac{\textsf{adjacent}}{\textsf{hypotenuse}} = \frac{7}{10}.\]
The opposite side to the angle \(a\) has length \(4\), and the hypotenuse has length \(10\), so by the definition of \(\sin\) you can say that \[\sin(a) = \frac{\textsf{opposite}}{\textsf{hypotenuse}} = \frac{4}{10} = \frac{2}{5}.\]
Finally, the opposite side to the angle \(b\) has length \(7\), and the adjacent side has length \(4\), so by the definition of \(\tan\) you can say that \[\tan(b) = \frac{\textsf{opposite}}{\textsf{adjacent}} = \frac{7}{4}.\]
The unit circle
The unit circle uses this relationship to represent the values of the trigonometric functions. The unit circle is a circle of radius one which is centered on the origin of a Cartesian coordinate system. Because of this, the radius represents the hypotenuse of the right angled triangle. Take \(\theta\) to be the angle as measured anticlockwise from the positive \(x\)-axis, and suppose that \((x,y)\) is a point on the unit circle.
If \(\theta\) is between \(0^\circ\) and \(90^\circ\), then the triangle created is right angled and the above definition for \(\sin\), \(\cos\), \(\tan\) applies. In this case, \(\cos(\theta)\) is equal to \(x\) and \(\sin(\theta)\) is equal to \(y\).
However, what if \(\theta\) is greater than \(90^\circ\)? Here’s an example.
Say you want to represent \(\sin(240^\circ)\) and \(\cos(240^\circ)\) on your unit circle. You would start with an unlabelled unit circle, marking on a line \(240^\circ\) from the positive \(x\)-axis. Now you want to make our triangle. In this case, you can draw a triangle where one side is the negative \(x\)-axis. Geometrically you can split the angle into the straight line and the excess which forms our triangle. That means our triangle ‘starts’ \(180^\circ\) away from the \(x\)-axis. This means that the angle in our triangle will be \(60^\circ\) radians.
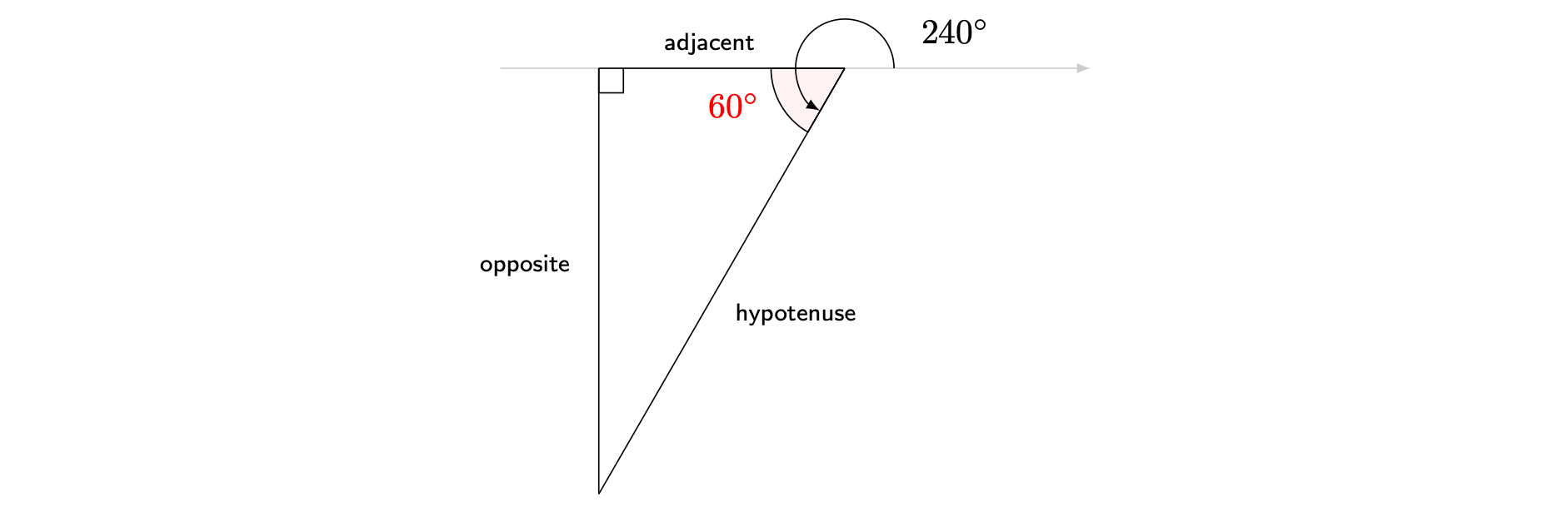
As you are using the unit circle, the hypotenuse will be equal to one. Then, you can label the opposite and adjacent sides as shown on the diagram above. As you know that \(\sin(\theta)=\frac{\textsf{opposite}}{\textsf{hypotenuse}}\) and \(\cos(\theta)=\frac{\textsf{adjacent}}{\textsf{hypotenuse}}\), you can see that the \(y\)-axis will represent \(\sin(\theta)\) and the \(x\)-axis \(\cos(\theta)\).
See Figure 3 for a picture of this angle on the unit circle.
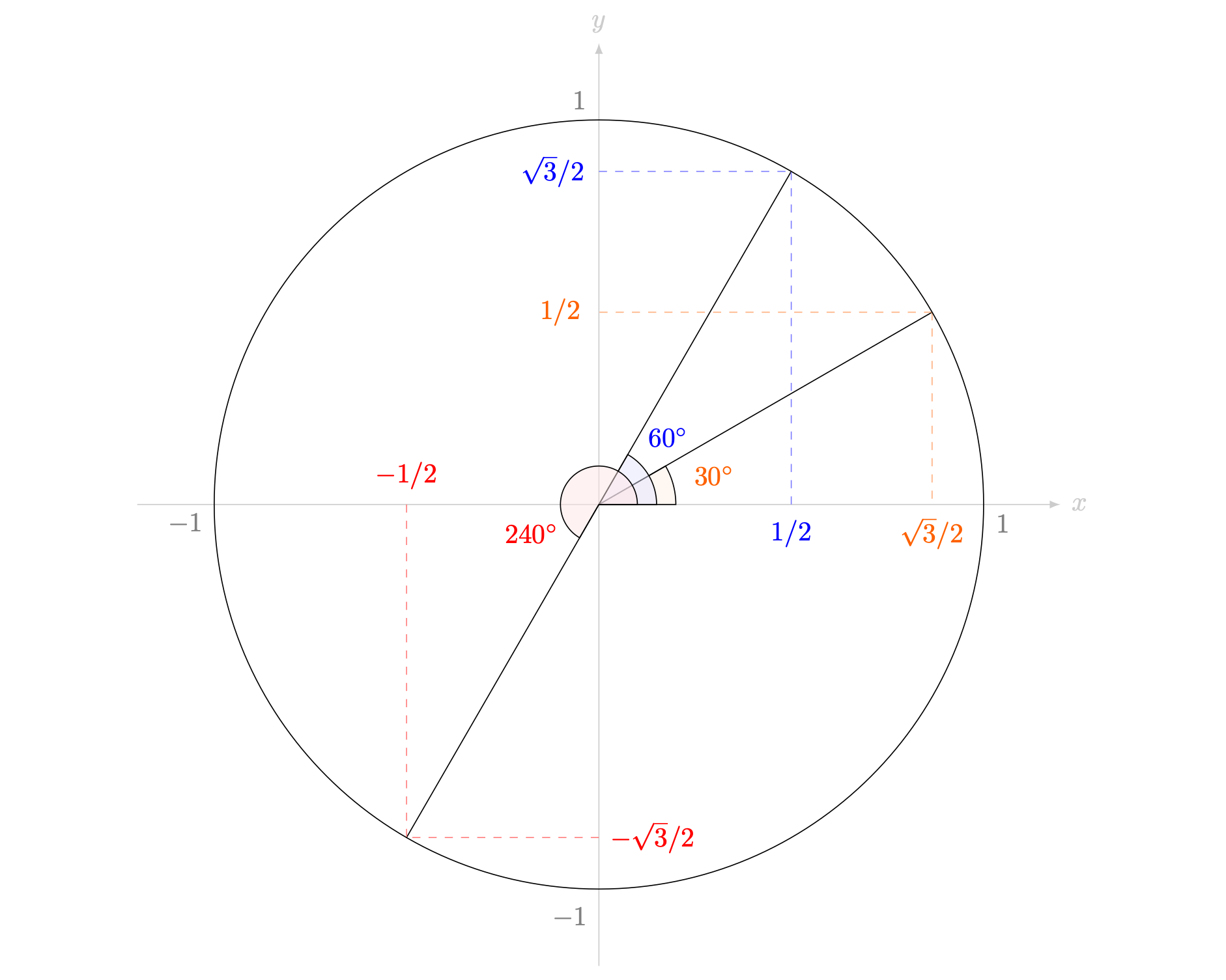
So from Example 1, the value of \(\sin(240^\circ)\) and \(\cos(240^\circ)\) are the \(y\)-axis and the \(x\)-axis respectively. Together with the discussion before Example 1, this leads to a new definition of the two trigonometric functions \(\sin\) and \(\cos\):
Let \((x,y)\) be a point on the unit circle centred at the origin \((0,0)\). Let \(\theta\) be the angle defined by the positive \(x\)-axis and the line segment from centre to the point \((x,y)\). Define \[\cos(\theta) = x \qquad \sin(\theta) = y\] and \[\tan(\theta) = \frac{y}{x} = \frac{\sin(\theta)}{\cos(\theta)}\]
This definition extends the trigonometric functions to situations outside right-angled triangles; dramatically increasing their usability. The figure below details how the values of \(\cos(t), \sin(t), \tan(t)\) change as the angle \(t\) changes.
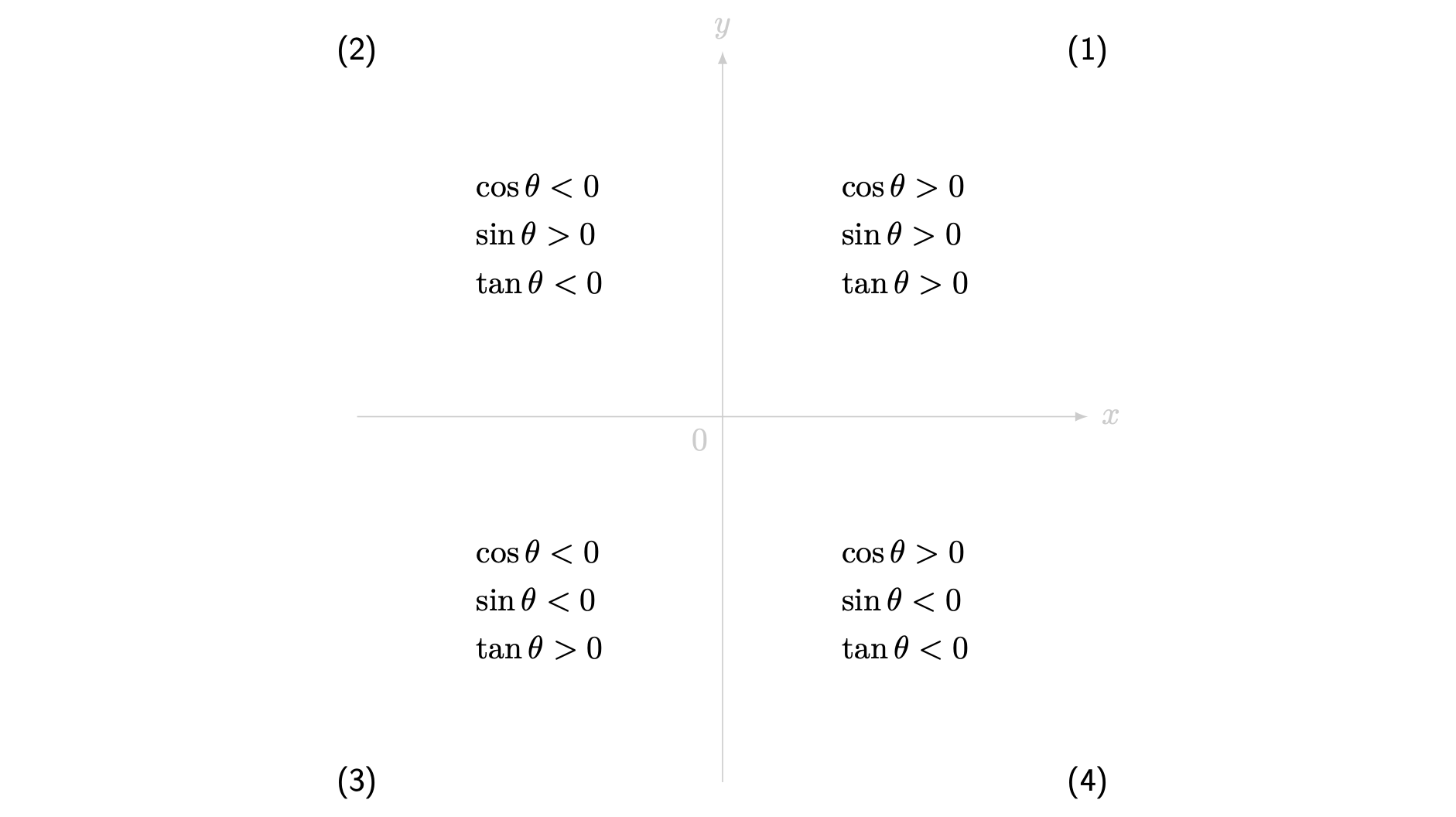
In the unit circle, the angle \(\theta\) ranges from \(0^\circ\) to \(360^\circ\). Over this range, the values of the co-ordinates \(x\) and \(y\) range from positive to negative. Therefore, the three main trigonometric functions \(\sin\), \(\cos\) and \(\tan\) take different signs in different positions.
If \(x > 0\) and \(y > 0\) (so \(0^\circ< \theta < 90^\circ\)), then both \(\cos(\theta) > 0\) and \(\sin(\theta) > 0\), and therefore \(\tan\theta > 0\).
If \(x < 0\) and \(y > 0\) (so \(90^\circ < \theta < 180^\circ\)), then \(\cos(\theta) < 0\) and \(\sin(\theta) > 0\), and therefore \(\tan(\theta) < 0\).
If \(x < 0\) and \(y < 0\) (so \(180^\circ < \theta < 270^\circ\)), then both \(\cos(\theta) < 0\) and \(\sin(\theta) < 0\), and therefore \(\tan(\theta) > 0\).
If \(x > 0\) and \(y < 0\) (so \(270^\circ < \theta < 360^\circ\)), then \(\cos(\theta) > 0\) and \(\sin(\theta) < 0\), and therefore \(\tan(\theta) < 0\).
See Figure 4 for a picture of this behaviour.
This analysis has missed out values of the three trigonometric functions on the axes. Here \(\theta=0^\circ\) along the positive \(x\)-axis, \(\theta=90^\circ\) along the positive \(y\)-axis, \(\theta=180^\circ\) along the negative \(x\)-axis, and \(\theta=270^\circ\) along the negative \(y\)-axis.
If \(\theta = 0^\circ\), then \(x = 1\) and \(y = 0\). Therefore \(\cos(0) = 1/1 = 1\) and \(\sin(0) = \tfrac{0}{1} = 0\) and so \(\tan(0) = \sin(0)/\cos(0) = 0/1 = 0\).
If \(\theta = 90^\circ\) (right angle of positive \(x\) and \(y\) axes) then \(x = 0\) and \(y = 1\). Therefore \(\cos(90^\circ) = 0/1 = 0\) and \(\sin(90^\circ) = 1/1 = 1\). In this case, \(\tan(90^\circ)\) is undefined as \(\cos(90^\circ) = 0\).
If \(\theta = 180^\circ\) (straight line, angle of positive \(x\) and negative \(x\) axes) then \(x = -1\) and \(y = 0\). Therefore \(\cos(180^\circ) = -1/1 = -1\) and \(\sin(180^\circ) = 0/1 = 0\). In this case, \(\tan(180^\circ) = \sin(180^\circ)/\cos(180^\circ) = 0/(-1) = 0\).
If \(\theta = 270^\circ\) (right angle of positive \(x\) and negative \(y\) axes) then \(x = 0\) and \(y = -1\). Therefore \(\cos \left(270^\circ\right) = 0/1 = 0\) and \(\sin\left(270^\circ\right) = -1/1 = -1\). In this case, \(\tan(270^\circ)\) is undefined as \(\cos (270^\circ) = 0\).
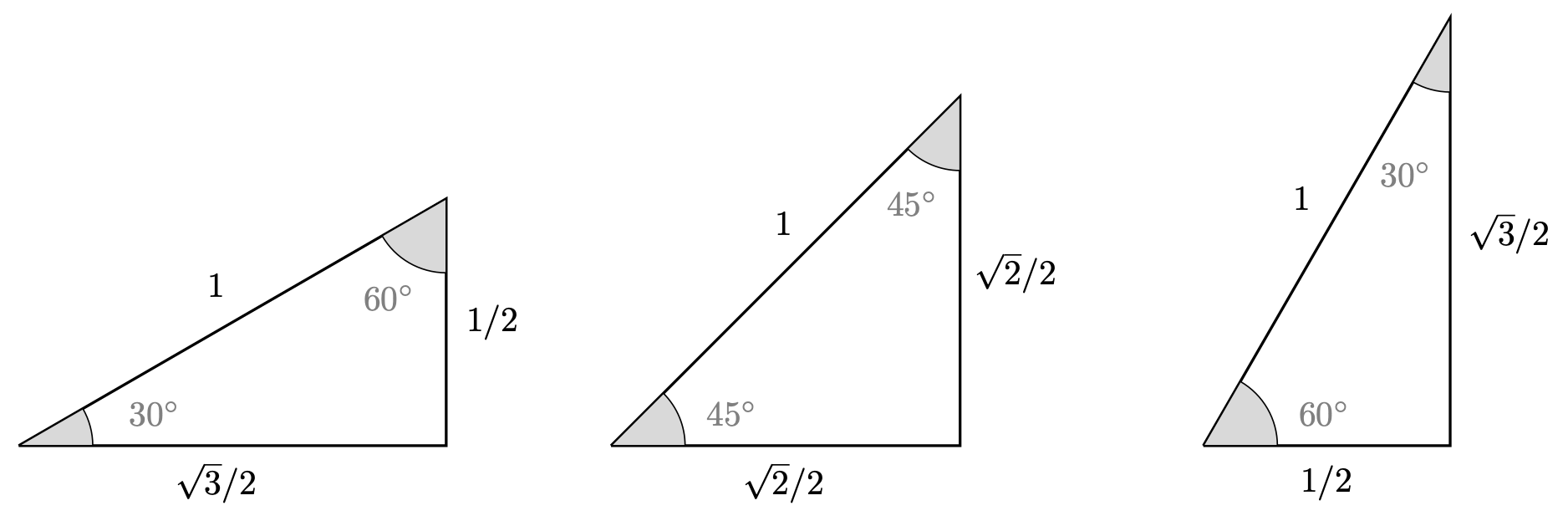
Table of common angles
When you solve problems you may need different values of these functions. For ease of use, mathematicians have created tables with most frequently used values.
| Angles (\(^\circ\)) | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | \(180^\circ\) | \(270^\circ\) |
|---|---|---|---|---|---|---|---|
| \(\sin(\theta)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(0\) | \(-1\) |
| \(\cos(\theta)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | \(0\) | \(-1\) | \(0\) |
| \(\tan(\theta)\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) | undef. | \(0\) | undef. |
These common values are also observed in the diagrams of three important triangles; see Figure 5 for more.
Reciprocals of trigonometric functions
In addition to \(\sin(\theta)\), \(\cos(\theta)\), and \(\tan(\theta)\), there are three more trigonometric functions known as the secant \(\sec(\theta)\), cosecant \(\csc(\theta)\) and cotangent which are defined in the following way:
\[\sec(\theta) = \frac{1}{\cos(\theta)} \qquad \csc(\theta) = \frac{1}{\sin(\theta)}\qquad \cot(\theta) = \frac{1}{\tan(\theta)}\]
Using the definition of \(\tan(\theta) = \sin(\theta)/\cos(\theta)\), you can also say that \[\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)}.\]
These, together with \(\sin\), \(\cos\) and \(\tan\), are known as the circular trigonometric functions. Of course, there is a health warning
What is \(\csc(45) + \cot(30) + \sec(60)\) equal to?
Using the definitions of \(\sec, \csc\) and \(\cot\), you can write \[\csc(45) + \cot(30) + \sec(60) = \frac{1}{\sin(45)} + \frac{1}{\tan(30)} + \frac{1}{\cos(60)}\] Using the table of known angles, and not forgetting to reciprocate, gives \[\begin{align*} \csc(45) + \cot(30) + \sec(60) &= \frac{1}{\sin(45)} + \frac{1}{\tan(30)} + \frac{1}{\cos(60)}\\[1em] &= \frac{1}{1/\sqrt{2}} + \frac{1}{1/\sqrt{3}} + \frac{1}{1/2} \\[1em] &= \sqrt{2} + \sqrt{3} + 2 \end{align*}\] and this is as far as you can go.
Prove that \(\displaystyle\frac{\sin(\theta)\cot(\theta)+\cos(\theta)}{2\cot(\theta)} = \sin(\theta)\).
Start with the left hand side. Using the definition of \(\cot(\theta)\) on the numerator and multiplying out, you can write that
\[\frac{\sin(\theta)\cot(\theta)+\cos(\theta)}{2\cot(\theta)} = \frac{\sin(\theta)\frac{\cos(\theta)}{\sin(\theta)}+\cos(\theta)}{2\cot(\theta)}= \frac{\cos(\theta)+\cos(\theta)}{2\cot(\theta)}\] Now collecting together the like terms on the numerator and using the definition of \(\cot(\theta)\) you can state that \[\frac{\cos(\theta)+\cos(\theta)}{2\cot(\theta)} = \frac{2\cos(\theta)}{2\frac{\cos(\theta)}{\sin(\theta)}} = \sin(\theta).\]
Quick check problems
If \(\sin(\theta)\) has the value \(\frac{\sqrt{2}}{2}\), does \(\cos(\theta)\) have the same value? Answer: .
You are given the following information on a right-angled triangle. The smallest side of the triangle has a length of three and for an angle \(\theta\) in the triangle, \(\tan(\theta) = \frac{3}{4}\). What size is the hypotenuse? Answer: The hypotenuse has a length of .
Which of the following is equal to \(\csc(60)\)?
Further reading
For more questions on the subject, please go to Questions: Trigonometry (degrees).
After this guide you may consider expanding your knowledge of trigonometry by reading Guide: Trigonometric identities (degrees) or Guide: Rearranging equations involving trigonometry and logarithms.
Guide: Trigonometry (radians) is a version of this guide using radians to measure angles.
Version history and licensing
v1.0: initial version created 08/23 by Dzhemma Ruseva, Ellie Gurini, Ciara Cormican as part of a University of St Andrews STEP project.
v1.1: edited 04/24 by tdhc, and split into versions for both degrees and radians.
v1.2: addition of interactive Desmos figures 01/25 by tdhc.