Introduction to vectors

Summary

Quantities expressing both a magnitude and a direction are called vectors. Vectors are used in various disciplines and have a wide range of real-life applications.

Introduction

Up until now, the quantities that you have studied in mathematics express ‘how much’ of something exists. For instance, you could have four apples, or be 178cm tall, or have £55 in your bank account. Even negative numbers can be used to represent ‘how much’; if you have -£55 in your bank account, you need to pay in £55 to get to zero again.

However, sometimes you need to use something different to express some physical quantities. For instance, suppose you were travelling somewhere to see a friend. It’s not enough to say you are travelling at 30mph — how do you know where you’ll meet? Similarly, saying that you’re going north-west isn’t useful; when will you meet your friend? Sometimes, you need quantities that possess both a magnitude (30mph) and a direction (north-west):

Definition of a vector

Any physical quantity that has both magnitude (size, or length) and direction is called a vector quantity.

Definition of a scalar

Any physical quantity that has magnitude only and no direction are called scalar quantities. Scalars are represented by a single number. They can be positive, negative or zero.

As the initial point of study in linear mathematics, vectors have various real-life applications across different fields, such as physics and engineering, navigation and GPS, computer graphics and gaming, data analysis and machine learning, cryptography, statistics and much more. In this guide, you will study some of the fundamental concepts about vectors, their algebraic and geometric properties, and an introduction to dealing with magnitude and unit vectors.

Note

Two vectors are said to be equal if they have the same magnitude and the same direction.

Initial properties of vectors

Free vectors

A vector can be any directed line in space. Here is a vector \(\mathbf{v}\).

Figure 1: A vector \(\mathbf{v}\)

Any vector defined in this way can be denoted by a bold letter \(\mathbf{v}\); or, if you are hand-writing, \(\underline{v}\). These are known as free vectors. A free vector \(\mathbf{v}\) can be ‘moved’ to have any start point in space, as long as the magnitude and the direction are preserved.

Figure 2: Many copies of the vector \(\mathbf{v}\)

Warning

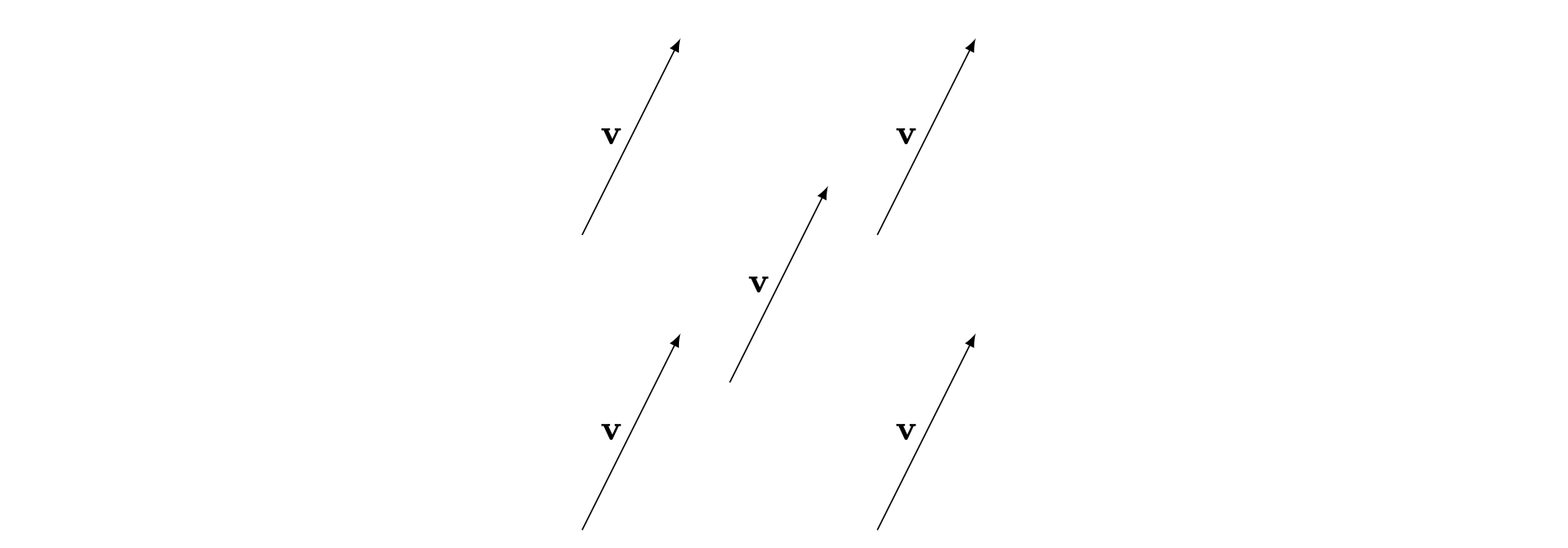
The reason that vectors are written in this way is to distinguish them from scalar quantities. You should always remember to underline vectors when doing your written work.

Note

This study guide will use the bold notation (\(\mathbf{a}\)). However, vectors can also be represented by using the arrow notation \(\vec{a}\) or (as previously mentioned) underlining them \(\underline{a}\).

Localized vectors

Another way to write a vector is to start and finish at two specified points in space. So consider a line segment \(AB\) in space and let a direction be assigned to it. The arrow marked on the line denotes the direction of the vector. The vector from \(A\) to \(B\) is written as \(\overrightarrow{AB}\). Any vector defined in this way is known as a localized vector, as the start point of the vector is a fixed point.

The direction in which the arrow points towards is called the head of a vector, which makes the other end the tail of the vector. The length of the line indicates the magnitude of the vector and is denoted by \(|\overrightarrow{AB}|\).

Figure 3: Graphical representation of the vector \(\overrightarrow{AB}\)

However, you could also consider the vector from \(B\) to \(A\), which is written as \(\overrightarrow{BA}\).

Figure 4: Graphical representation of the vector \(\overrightarrow{BA}\)

Any free vector can be turned into a localized vector by specifying a start point. Any localized vector can be turned into a free vector by ‘forgetting’ the start point. See below for some examples.

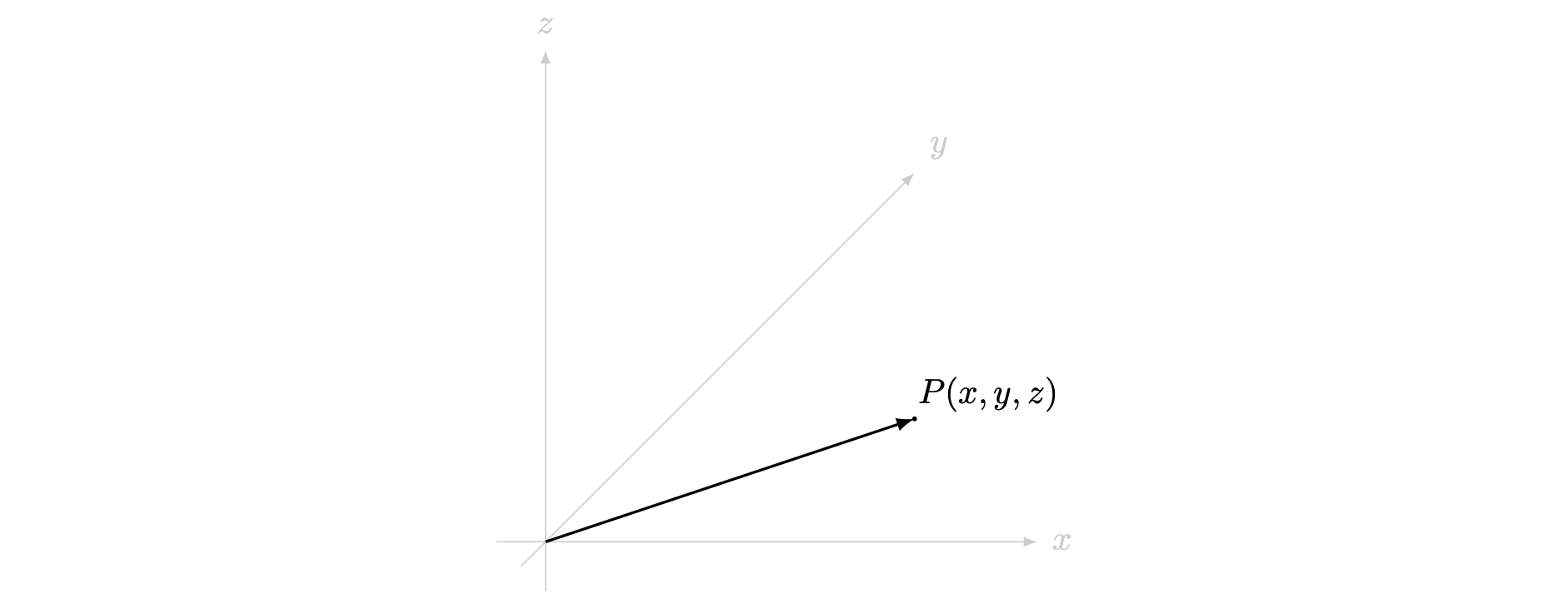
Any localized vector that starts at the origin \(O = (0,0,0)\) of three dimensional space is known as a position vector; as this vector specifies a point in space. Every free vector can be viewed as a position vector.

Figure 5: The position vector for the point \(P\) with respect to the origin

Negative vectors

Here, you can notice that the direction of \(\overrightarrow{BA}\) is exactly opposite to the direction of \(\overrightarrow{BA}\), but with the same magnitude. Therefore, you could write \(\overrightarrow{BA} = -\overrightarrow{AB}\); in fact, this is the exact definition of the negative of a vector.

Negative of a vector

Let \(\mathbf{a}\) be a vector. The vector whose magnitude is the same as that of \(\mathbf{a}\) but is in exactly the opposite direction is called the negative of \(\mathbf{a}\) and is written \(-\mathbf{a}\).

Scaling vectors

You can notice that the negative of a vector \(\mathbf{a}\) is written as \(-\mathbf{a}\), which is the same as \((-1)\mathbf{a}\). This is a special example of more general behaviour, known as scalar multiplication of vectors.

Scalar multiplying a vector by a positive scalar changes the magnitude of the vector and preserves the direction, and multiplying a vector by a negative scalar changes the magnitude of the vector and reverses the direction.

Example 1

Let \(\overrightarrow{AB}\) be a vector. Then \(2\overrightarrow{AB}\) is a vector in the same direction as \(\overrightarrow{AB}\) but twice as long, and \(-3\overrightarrow{AB}\) is a vector in the opposite direction as \(\overrightarrow{AB}\) (so the same direction as \(\overrightarrow{BA}\)) and three times as long.

Similarly, \(\frac{1}{2}\overrightarrow{BA}\) is a vector in the same direction as \(\overrightarrow{BA}\), but half as long. Since the magnitudes of \(\overrightarrow{AB}\) and \(\overrightarrow{BA}\) are the same, it follows that this vector is also half the length of \(\overrightarrow{AB}\).

Warning

You cannot multiply together two vectors, only a vector and a scalar.

For more on scalar multiplication on vectors, please see Guide: Vector addition and scalar multiplication.

Finally, there is one special vector that possesses a zero magnitude.

Definition of the zero vector

A vector is said to be the zero vector or null vector if its magnitude is zero. The zero vector is usually written as \(\mathbf{0}\) (or, if you are handwriting, \(\underline{0}\)).

For any vector \(\mathbf{v}\), it can be shown that \(0\mathbf{v} = \mathbf{0}\).

Vectors in three-dimensional space

A vector \(\mathbf{a}\) can be expressed in both two-dimensional and three-dimensional space through various coordinate systems. You will see the standard Cartesian coordinate system in this guide.

i,j,k notation

In three-dimensional space, \(\mathbf{i}\), \(\mathbf{j}\), \(\mathbf{k}\) are the vectors with magnitude \(1\) pointing in the positive direction along the \(x\)-axis, \(y\)-axis and \(z\)-axis respectively. Any vector in the three-dimensional Cartesian coordinate system can be generally represented as a sum of scalar multiples of these three vectors \(\mathbf{i}\), \(\mathbf{j}\), \(\mathbf{k}\). Any such combination of vectors is known as a linear combination.

Figure 6: \(\mathbf{i},\mathbf{j},\mathbf{k}\) unit vectors along their respective axis.

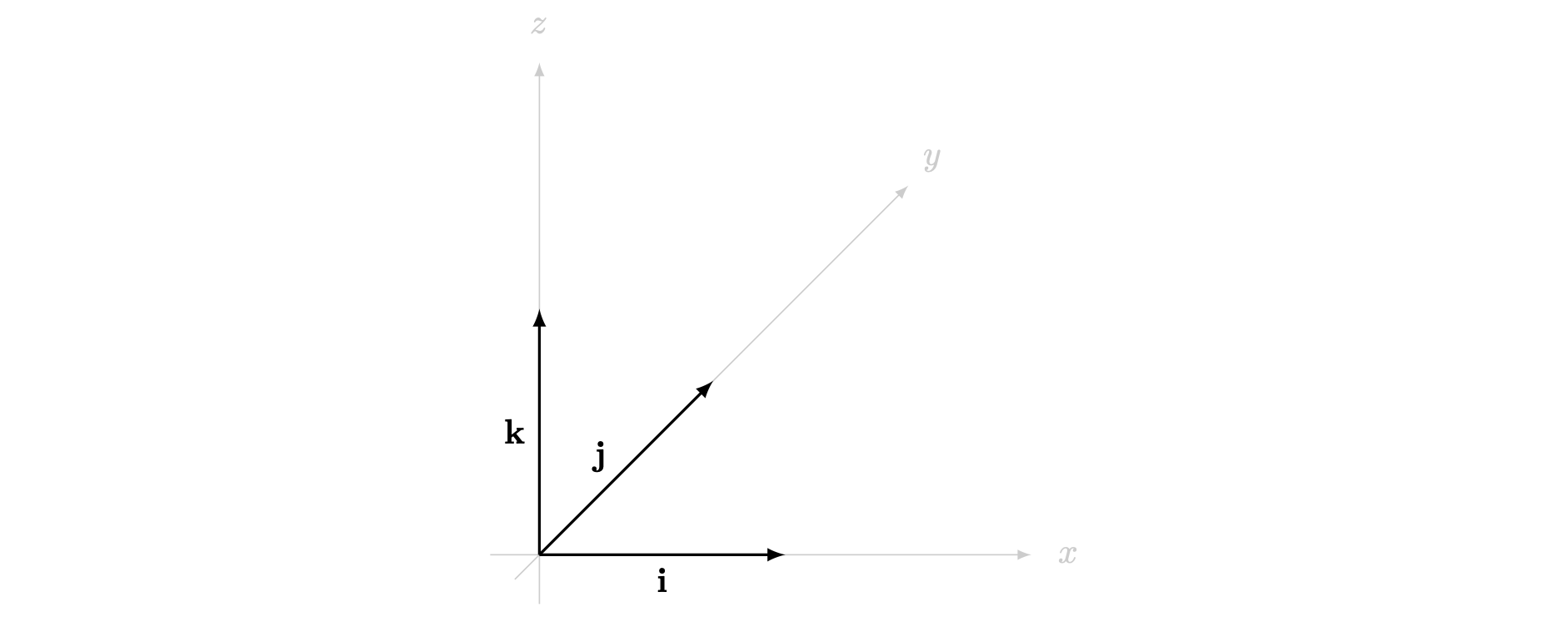
Following this, any vector \(\mathbf{a}\) can be expressed in the format

\[\mathbf{a}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\]

where \(x\) is the coefficient of the vector along the \(\mathbf{i}\)-direction, \(y\) is the coefficient along the \(\mathbf{j}\)-direction, and \(z\) is the coefficient along the \(\mathbf{k}\)-direction. These coefficients are known as components of the vector: for example, \(x\) is the \(\mathbf{i}\)-component of the vector \(\mathbf{a}\).

Here, a positive \(x\) is along the positive \(x\)-axis, whereas the vectors towards the negative \(x\)-axis would have a negative \(x\) value. The same is true for the other two axes as well.

Example 2

You are given a vector \(\mathbf{a}=2\mathbf{i}+5\mathbf{j}+4\mathbf{k}\). This means that the vector \(\mathbf{a}\) is a free vector moving \(2\) units along the positive \(x\)-axis, \(5\) units along the positive \(y\)-axis and \(4\) units along the positive \(z\)-axis.

As \(\mathbf{a}\) is a free vector, you can start \(\mathbf{a}\) at any point. Starting the vector \(\mathbf{a}\) at the origin defines the line segment from \((0,0,0)\) to \((2,5,4)\) in three dimensional space; therefore, \(\mathbf{a}\) is the position vector of the point \((2,5,4)\).

Example 3

You are given a vector \(\mathbf{b}=-7\mathbf{k}+3\mathbf{i}\). This means that the vector \(\mathbf{b}\) is a free vector with \(\mathbf{i}\) component \(3\), \(\mathbf{j}\) component \(0\) and \(\mathbf{k}\) component \(-7\).

Example 4

You are given the vector \(\overrightarrow{AB}\) where \(A = (3,4,5)\) and \(B = (4,-3,5)\) are two points in three dimensional space. You can write \(\overrightarrow{AB}\) in \(\mathbf{i}\), \(\mathbf{j}\), \(\mathbf{k}\) notation by considering the distances moved between each of the co-ordinates.

• The \(x\)-coordinate of \(A\) is \(3\) and the \(x\)-coordinate of \(B\) is \(4\). The difference from \(B\) to \(A\) is \(4-3 = 1\), and so the vector has \(\mathbf{i}\) component \(1\).
• The \(y\)-coordinate of \(A\) is \(4\) and the \(y\)-coordinate of \(B\) is \(-3\). The difference from \(B\) to \(A\) is \(-3-4 = -7\), and so the vector has \(\mathbf{j}\) component \(-7\).
• The \(z\)-coordinate of \(A\) is \(5\) and the \(z\)-coordinate of \(B\) is \(5\). The difference from \(B\) to \(A\) is \(5-5 = 0\), and so the vector has \(\mathbf{k}\) component \(0\).

Therefore, \(\overrightarrow{AB} = 1\mathbf{i} + (-7)\mathbf{j} + (0)\mathbf{k} = \mathbf{i} - 7\mathbf{j}\).

Column vector notation

This is another way of representing vectors. A column vector is a vector whose components are listed vertically in a single column, with the \(\mathbf{i}\) component at the top, the \(\mathbf{j}\) component in the middle and the \(\mathbf{k}\) component at the bottom.

So, a vector \(\mathbf{a}\) can be written as:

\[\mathbf{a}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}=\begin{pmatrix}x\\y\\z\end{pmatrix}\]

Example 5

You are given the vector \(\mathbf{c}=3\mathbf{i}-4\mathbf{j}+5\mathbf{k}\). To represent this vector in column notation you can write the components of the vector as specified above. So, \[\mathbf{c}=3\mathbf{i}-4\mathbf{j}+5\mathbf{k}=\begin{pmatrix}3\\-4\\5\end{pmatrix}.\]

Example 6

To express the vector \(\displaystyle \mathbf{d}=\begin{pmatrix}-7\\0\\4\end{pmatrix}\) in terms of \(\mathbf{i},\mathbf{j},\mathbf{k}\), you can reverse the process given above to write \[\mathbf{d}=\begin{pmatrix}-7\\0\\4\end{pmatrix}=(-7)\mathbf{i}+0\mathbf{j}+4\mathbf{k} = -7\mathbf{i} + 4\mathbf{k}.\]

Note

How do you express the zero vector \(\mathbf{0}\) in both of these vector notations? Here, the values of each of the components of the zero vector are \(0\), so \[\mathbf{0} = 0\mathbf{i} + 0\mathbf{j} + 0\mathbf{k} = \begin{pmatrix}0\\0\\0\end{pmatrix}.\]

How do you express the negative of a vector \(\mathbf{a} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k} = \begin{pmatrix}x\\y\\z\end{pmatrix}\)? The negative of a vector is its reverse; so all of the components are multiplied by \(-1\). Therefore \[-\mathbf{a} = (-x)\mathbf{i} + (-y)\mathbf{j} + (-z)\mathbf{k} = \begin{pmatrix}-x\\-y\\-z\end{pmatrix}.\]

Finally, when are two vectors in our notation equal? Let \(\mathbf{a} = a_1 \mathbf{i} + a_2 \mathbf{j} + a_3 \mathbf{k}\) and \(\mathbf{b} = b_1 \mathbf{i} + b_2 \mathbf{j} + b_3 \mathbf{k}\). These two vectors are equal if and only if they have the same direction and the same magnitude; so all the components must match. That is, \[\mathbf{a} = \mathbf{b}\quad\textsf{ if and only if }\quad a_1 = b_1,\, a_2 = b_2,\, a_3 = b_3.\]

Magnitudes and unit vectors

Since any free vector \(\mathbf{a}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) can be viewed as a position vector for the point \((x,y,z)\), the magnitude of the vector \(\mathbf{a}\) is the same as the distance from the origin \((0,0,0)\) to the point \((x,y,z)\). This gives:

Magnitude of a vector

Let \(\displaystyle\mathbf{a} = x\mathbf{i}+y\mathbf{j}+z\mathbf{k} = \begin{pmatrix}x\\y\\z\end{pmatrix}\) be a vector. The magnitude of \(\mathbf{a}\) is given by \[|\mathbf{a}| = \sqrt{x^2 + y^2 + z^2}\]

Warning

The magnitude of a vector is always non-negative.

Example 7

You are given the two vectors \(\mathbf{p}=\mathbf{i}+4\mathbf{j}-8\mathbf{k}\) and \(\mathbf{q} = -4\mathbf{i}+2\mathbf{j}+11\mathbf{k}\). What are their magnitudes?

You can use the formula for the magnitude of a vector as given above. For the vector \(\mathbf{p}\), this is where the \(\mathbf{i}\) component is \(1\), the \(\mathbf{j}\) component is \(4\), and the \(\mathbf{k}\) component is \(-8\). So \[|\mathbf{p}|= \sqrt{(1)^2 + (4)^2 + (-8)^2} = \sqrt{1+16+64} = \sqrt{81} = 9\]

Similarly, the magnitude for \(\mathbf{q} = =-4\mathbf{i}+2\mathbf{j}+11\mathbf{k}\) is \[|\mathbf{q}| = \sqrt{(-4)^2 + (2)^2 + (11)^2} = \sqrt{16 + 4 + 121} = \sqrt{141}\]

Since the magnitude of a vector \(\mathbf{a}\) is a scalar, you can scalar multiply by \(1/|\mathbf{a}|\), which is the same as dividing the vector \(\mathbf{a}\) by \(|\mathbf{a}|\). As scalar multiplication does not change the direction of a vector, the vector \(\mathbf{a}/|\mathbf{a}|\) has the same direction as \(\mathbf{a}\) and magnitude \(|\mathbf{a}|/|\mathbf{a}| = 1\). This has a special name:

Unit vector

Any vector with a magnitude equal to \(1\) is called a unit vector.

Unit vectors can be constructed in any direction. Let \(\displaystyle\mathbf{a} = x\mathbf{i}+y\mathbf{j}+z\mathbf{k} = \begin{pmatrix}x\\y\\z\end{pmatrix}\) be a vector. The unit vector \(\hat{\mathbf{a}}\) in the direction of \(\mathbf{a}\) is given by \[\hat{\mathbf{a}}=\frac{\mathbf{a}}{|\mathbf{a}|}=\frac{x\mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{x^2+y^2+z^2}}\]

For example, the co-ordinate vectors \(\mathbf{i},\mathbf{j},\mathbf{k}\) are all unit vectors, since they are defined to have magnitude \(1\).

Example 8

Remember the two vectors \(\mathbf{p}=\mathbf{i}+4\mathbf{j}-8\mathbf{k}\) and \(\mathbf{q} = -4\mathbf{i}+2\mathbf{j}+11\mathbf{k}\) from Example 7. What are the unit vectors in the directions of \(\mathbf{p}\) and \(\mathbf{q}\)?

You worked out in Example 7 that the magnitude of \(\mathbf{p}\) is \(|\mathbf{p}| = 9\). Therefore, the unit vector in the direction of \(\mathbf{p}\) is \[\hat{\mathbf{p}} = \frac{\mathbf{p}}{|\mathbf{p}|} = \frac{\mathbf{i}+4\mathbf{j}-8\mathbf{k}}{9} = \frac{1}{9}\left(\mathbf{i}+4\mathbf{j}-8\mathbf{k}\right)\]

Similarly, you worked out in Example 7 that the magnitude of \(\mathbf{q}\) is \(|\mathbf{q}| = \sqrt{141}\). Therefore, the unit vector in the direction of \(\mathbf{q}\) is \[\hat{\mathbf{q}} = \frac{\mathbf{q}}{|\mathbf{q}|} = \frac{1}{\sqrt{141}}\left(-4\mathbf{i}+2\mathbf{j}+11\mathbf{k}\right)\]

Quick check problems

1. State whether these statements are true or false.

   1. The magnitude of a vector is always a non-negative value. Answer: TRUEFALSE.

   2. The zero vector has a magnitude of one. Answer: TRUEFALSE.

   3. If \(\mathbf{v}\) is a non-zero vector, then there exists a unit vector in the direction of \(\mathbf{v}\). Answer: TRUEFALSE.

2. If \(\mathbf{a}=\begin{pmatrix}2\\-2\\-1\end{pmatrix}\), then what is \(|\mathbf{a}|\)?

   Answer: \(|\mathbf{a}|\) is equal to .

3. Find the unit vector in the direction of \(\mathbf{b}=-3\mathbf{i}+4\mathbf{k}\). (Give your answers using decimals.)

   Answer: \(\hat{\mathbf{b}}\) is equal to \(\mathbf{i}+\)\(\mathbf{k}\).

Further reading

For more questions on this topic, please go to Questions: Introduction to vectors.

To explore more about vectors, included how they are added and scalar multiplied, please see either Guide: Vector addition and scalar multiplication.

Version history and licensing

v1.0: initial version created 08/23 by Akshat Srivastava as part of a University of St Andrews STEP project.

• v1.1: edited 05/24 by tdhc.

This work is licensed under CC BY-NC-SA 4.0.