Questions: Trigonometry (radians)
Before attempting these questions, it is recommended that you read Guide: Trigonometry (radians)
Q1
You are given the triangle below.
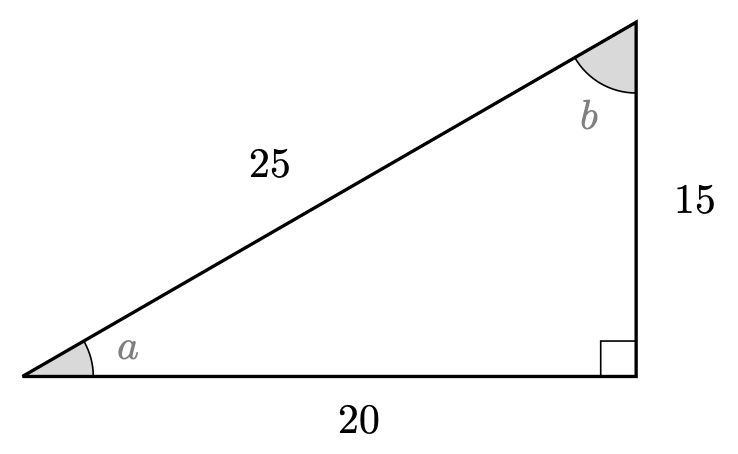
Find \(\cos\), \(\sin\) and \(\tan\) of both \(a\) and \(b\).
Q2
Using the triangle below, solve the following equations.
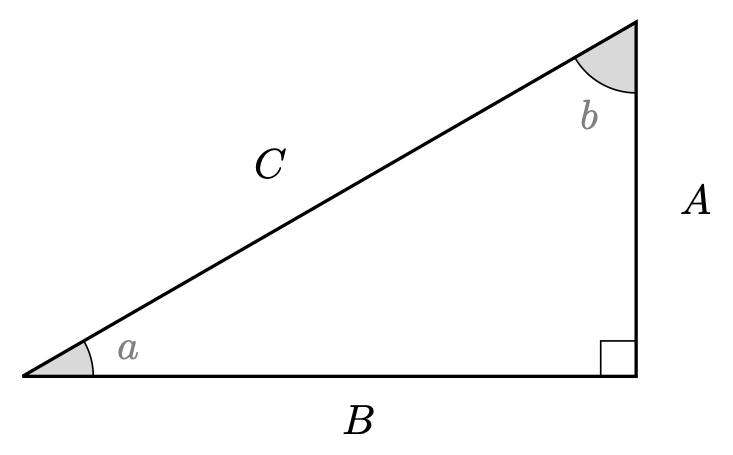
2.1. If angle \(a\) is \(\pi/6\) and \(B = 6\), what length is \(C\)?
2.2. If angle \(b\) is \(\pi/4\) and \(C = 2\sqrt{2}\), what length is \(A\)?
2.3. If angle \(a\) is \(\pi/12\) and \(C = 7\), what length is \(A\)?
2.4. If angle \(b\) is \(\pi/6\) and \(C = 2\sqrt{2}\), what length is \(A\)?
2.5. If angle \(a\) is \(\pi/4\) and \(B = 8\), what length is \(A\)?
2.6. If angle \(a\) is \(\pi/3\) and \(A = 8\), what length is \(B\)?
Q3
Without using a calculator if possible, give the values of the following expressions.
3.1. \(\cos(\pi/6)\)
3.2. \(\tan(\pi/6)\)
3.3. \(\csc(\pi/4)\)
3.4. \(\cot(\pi/6) - \sin(\pi/3)\)
3.5. \(\sin(\pi/2) + \cos(\pi)\)
3.6. \(\tan(\pi/6) - \cot(\pi/6)\)
3.7. \(\cos(0)\sin(\pi/2)\)
3.8. \(\cos(\pi/6)\sec(\pi/6) - \sin(\pi/4)\csc(\pi/4)\)
3.9. \(\cot(\pi/2)\)
After attempting the questions above, please click this link to find the answers.
Version history and licensing
v1.0: initial version created 08/23 by Dzhemma Ruseva, Ellie Gurini, Ciara Cormican as part of a University of St Andrews STEP project.
- v1.1: edited 05/24 by tdhc, and split into versions for both degrees and radians.