Answers: Trigonometry (radians)

Summary

Answers to the questions on trigonometry, using radians to measure angles.

These are the answers to Questions: Trigonometry (radians).

Please attempt the questions before reading these answers!

Q1

You are given the triangle below.

Q1. Triangle

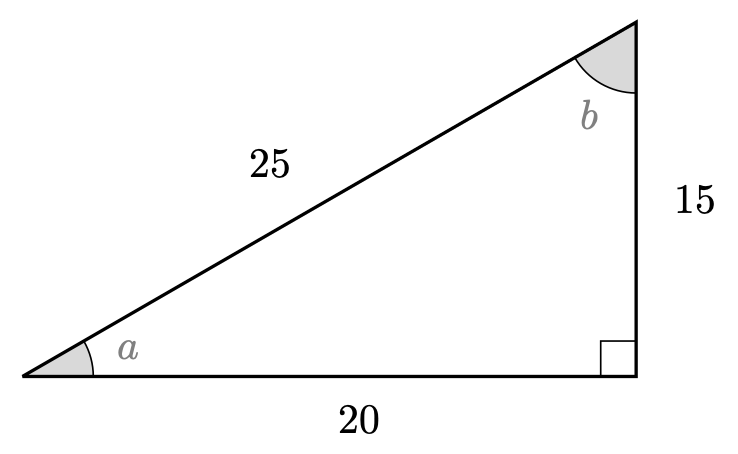
Here,

• \(\cos(a) = \dfrac{4}{5}\)

• \(\sin(a) = \dfrac{3}{5}\)

• \(\tan(a) = \dfrac{3}{4}\)

• \(\cos(b) = \dfrac{3}{5}\)

• \(\sin(b) = \dfrac{4}{5}\)

• \(\tan(b) = \dfrac{4}{3}\)

Q2

Using the triangle below, solve the following equations.

Q2. Triangle

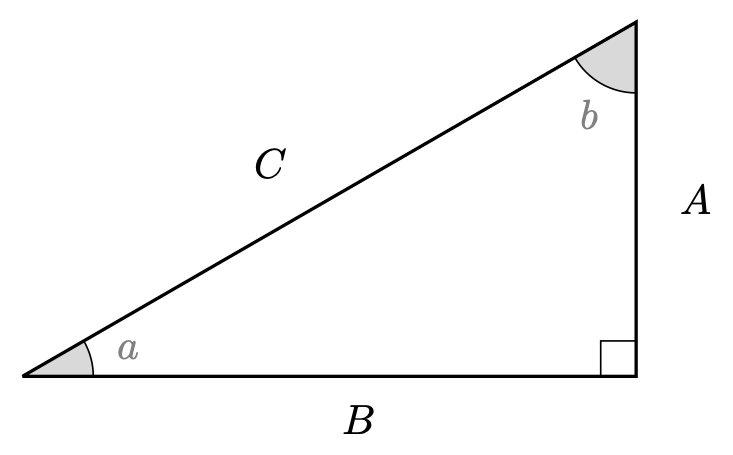
2.1. \(C = 12\)

2.2. \(A = 2\)

2.3. \(A = 1.812\) (to three decimal places)

2.4. \(A = \sqrt{6}\)

2.5. \(A = 8\)

2.6. \(B = \frac{8}{\sqrt{3}}\).

Q3

3.1. \(\cos(\pi/6) = \dfrac{\sqrt{3}}{2}\)

3.2. \(\tan(\pi/6) = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}\)

3.3. \(\csc(\pi/4) = 1\)

3.4. \(\cot(\pi/6) - \sin(\pi/3) = \sqrt{3} - \dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{3}}{2}\)

3.5. \(\sin(\pi/2) + \cos(\pi) = 1 + (-1) = 0\)

3.6. \(\tan(\pi/6) - \cot(\pi/6) = \frac{1}{\sqrt{3}} - \sqrt{3}\)

3.7. \(\cos(0)\sin(\pi/2) = 1\cdot 1 = 1\)

3.8. \(\cos(\pi/6)\sec(\pi/6) - \sin(\pi/4)\csc(\pi/4) = 1 - 1 = 0\)

3.9. \(\cot(\pi/2) = 0\)

---

---

Version history and licensing

v1.0: initial version created 08/23 by Dzhemma Ruseva, Ellie Gurini, Ciara Cormican as part of a University of St Andrews STEP project.

• v1.1: edited 05/24 by tdhc, and split into versions for both degrees and radians.

This work is licensed under CC BY-NC-SA 4.0.